题目内容
已知长为m(m>0)的线段P1P2两端点上在y2=4x上移动.(1)求P1P2中点M的轨迹方程;
(2)求M点到y轴距离的最小值及对应点M的坐标.
【答案】分析:(1)设P1(t12,2t1),P2(t22,2t2),P1P2中点为M(x,y),利用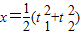 ,y=t1+t2,|P1P2|=m,消去t1,t2 即可得到中点的轨迹方程.
,y=t1+t2,|P1P2|=m,消去t1,t2 即可得到中点的轨迹方程.
(2)通过中点轨迹方程,m≥4,m<4,求出M点到y轴距离的最小值及对应点M的坐标.
解答:解:(1)设P1(t12,2t1),P2(t22,2t2),P1P2中点为M(x,y),则
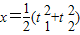 …①y=t1+t2…②
…①y=t1+t2…②
而|P1P2|=m∴(t12-t22)2+(2t1-2t2)2=m2…③
由①,②,③(4x-y2)(y2+4)=m2…④
这就是P1P2中点的轨迹方程.
(2)由④: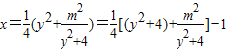 .
.
∵y2+4∈[4,+∞)
当m≥4时,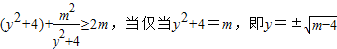 时,
时,
取“=”号.此时: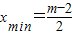 .M点的坐标为
.M点的坐标为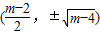 .
.
当m<4时,由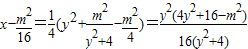
∵0<m<4∴
此时,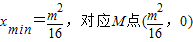
∴当m≥4时,M到y轴距离最小值为 ,M点坐标为
,M点坐标为 .
.
当0<m<4时,M到y轴距离最小值为
点评:本题是中档题,考查曲线的轨迹方程的求法,考查计算能力,转化思想,函数最值的求法.
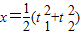 ,y=t1+t2,|P1P2|=m,消去t1,t2 即可得到中点的轨迹方程.
,y=t1+t2,|P1P2|=m,消去t1,t2 即可得到中点的轨迹方程.(2)通过中点轨迹方程,m≥4,m<4,求出M点到y轴距离的最小值及对应点M的坐标.
解答:解:(1)设P1(t12,2t1),P2(t22,2t2),P1P2中点为M(x,y),则
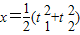 …①y=t1+t2…②
…①y=t1+t2…②而|P1P2|=m∴(t12-t22)2+(2t1-2t2)2=m2…③
由①,②,③(4x-y2)(y2+4)=m2…④
这就是P1P2中点的轨迹方程.
(2)由④:
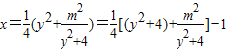 .
.∵y2+4∈[4,+∞)
当m≥4时,
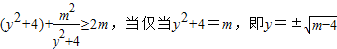 时,
时,取“=”号.此时:
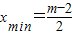 .M点的坐标为
.M点的坐标为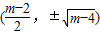 .
.当m<4时,由
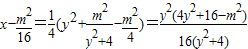
∵0<m<4∴

此时,
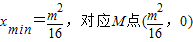
∴当m≥4时,M到y轴距离最小值为
 ,M点坐标为
,M点坐标为 .
.当0<m<4时,M到y轴距离最小值为

点评:本题是中档题,考查曲线的轨迹方程的求法,考查计算能力,转化思想,函数最值的求法.

练习册系列答案
相关题目