题目内容
设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和.,求ξ分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若Eη=
,Dη=
,求a:b:c.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和.,求ξ分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若Eη=
| 5 |
| 3 |
| 5 |
| 9 |
(1)由题意得ξ=2,3,4,5,6,
P(ξ=2)=
=
;P(ξ=3)=
=
;P(ξ=4)=
=
;
P(ξ=5)=
=
;P(ξ=6)=
=
.
故所求ξ的分布列为
(2)由题意知η的分布列为
Eη=
+
+
=
Dη=(1-
)2
+(2-
)2
+(3-
)2
=
.
得
,
解得a=3c,b=2c,
故a:b:c=3:2:1.
P(ξ=2)=
| 3×3 |
| 6×6 |
| 1 |
| 4 |
| 2×3×2 |
| 6×6 |
| 1 |
| 3 |
| 2×3×1+2×2 |
| 6×6 |
| 5 |
| 18 |
P(ξ=5)=
| 2×2×1 |
| 6×6 |
| 1 |
| 9 |
| 1×1 |
| 6×6 |
| 1 |
| 36 |
故所求ξ的分布列为
| ξ | 2 | 3 | 4 | 5 | 6 | ||||||||||
| P |
|
|
|
|
|
| η | 1 | 2 | 3 | ||||||
| P |
|
|
|
| a |
| a+b+c |
| 2b |
| a+b+c |
| 3c |
| a+b+c |
| 5 |
| 3 |
Dη=(1-
| 5 |
| 3 |
| a |
| a+b+c |
| 5 |
| 3 |
| b |
| a+b+c |
| 5 |
| 3 |
| c |
| a+b+c |
| 5 |
| 9 |
得
|
解得a=3c,b=2c,
故a:b:c=3:2:1.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
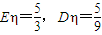 ,求a:b:c.
,求a:b:c.