题目内容
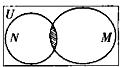已知全集U=R，集合M={x∈R|-2≤x-1≤2}，N={x|x=2k，k∈Z}的关系的韦恩（Venn）图如图所示，则阴影部分所示的集合的元素共有（ ）分析：根据韦恩图的可判断图中阴影部分表示集合M∩N；结合已知中，集合M，N及集合的交集运算，求出M∩N后，可得答案．
解答：解：图中阴影部分所示的集合为M∩N
∵M={x∈R|-2≤x-1≤2}={x∈R|-1≤x≤3}，且N={x|x=2k，k∈Z}，
∴M∩N={0，2}
故阴影部分所示的集合的元素共有2个
故选B
∵M={x∈R|-2≤x-1≤2}={x∈R|-1≤x≤3}，且N={x|x=2k，k∈Z}，
∴M∩N={0，2}
故阴影部分所示的集合的元素共有2个
故选B
点评：本题以集合元素个数判断为载体考查了集合的韦恩图表示法，及集合交集的运算，正确理解图示阴影部分表示的集合是解答的关键．
练习册系列答案
相关题目