题目内容
已知 与
与 为互相垂直的单位向量,
为互相垂直的单位向量, ,
, 且
且 与
与 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( )A.(-∞,-2)

B.(
 ,+∞)
,+∞)C.(-2,
 )
)
D.(-
 )
)
【答案】分析:本题考查的知识点是平面向量数量积的运算,由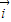 与
与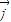 为互相垂直的单位向量,我们易得
为互相垂直的单位向量,我们易得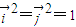 ,
,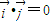 ,代入
,代入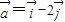 ,
,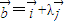 可求出
可求出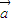 •
•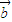 ,又由
,又由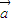 与
与 的夹角为锐角,故
的夹角为锐角,故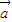 •
•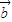 >0,由此得到一个关于λ的不等式,解不等式即可得到实数λ的取值范围,但要注意,
>0,由此得到一个关于λ的不等式,解不等式即可得到实数λ的取值范围,但要注意,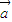 与
与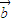 同向的排除.
同向的排除.
解答:解:∵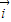 与
与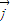 为互相垂直的单位向量
为互相垂直的单位向量
∴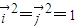 ,
,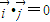 ,
,
又∵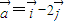 ,
,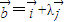
且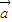 与
与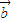 的夹角为锐角,
的夹角为锐角,
∴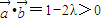 ,
,
但当λ=-2时,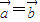 ,不满足要求
,不满足要求
故满足条件的实数λ的取值范围是(-∞,-2)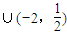
故选A
点评:两个向量夹角为锐角,则两个向量的数量积为正;
两个向量夹角为钝角,则两个向量的数量积为负;
两个向量夹角为直角,则两个向量的数量积为零;
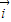 与
与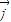 为互相垂直的单位向量,我们易得
为互相垂直的单位向量,我们易得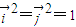 ,
,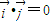 ,代入
,代入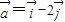 ,
,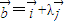 可求出
可求出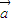 •
•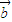 ,又由
,又由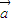 与
与 的夹角为锐角,故
的夹角为锐角,故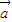 •
•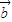 >0,由此得到一个关于λ的不等式,解不等式即可得到实数λ的取值范围,但要注意,
>0,由此得到一个关于λ的不等式,解不等式即可得到实数λ的取值范围,但要注意,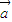 与
与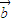 同向的排除.
同向的排除.解答:解:∵
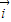 与
与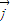 为互相垂直的单位向量
为互相垂直的单位向量∴
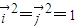 ,
,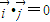 ,
,又∵
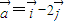 ,
,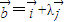
且
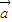 与
与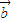 的夹角为锐角,
的夹角为锐角,∴
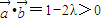 ,
,但当λ=-2时,
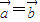 ,不满足要求
,不满足要求故满足条件的实数λ的取值范围是(-∞,-2)
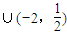
故选A
点评:两个向量夹角为锐角,则两个向量的数量积为正;
两个向量夹角为钝角,则两个向量的数量积为负;
两个向量夹角为直角,则两个向量的数量积为零;

练习册系列答案
相关题目
 与
与 为互相垂直的单位向量,
为互相垂直的单位向量, ,
, 且
且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 与
与 为互相垂直的单位向量,
为互相垂直的单位向量, ,
, 且
且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是( )
的取值范围是( )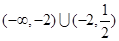 B.
B.
 D.
D.
 与
与 为互相垂直的单位向量,
为互相垂直的单位向量, ,
, 且
且 与
与 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( )
 ,+∞)
,+∞) )
)
 )
) 与
与 为互相垂直的单位向量,
为互相垂直的单位向量, ,
,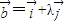 且
且 与
与 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( )
 ,+∞)
,+∞) )
)
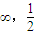 )
)