题目内容
已知如图所示正方体ABCD－A1B1C1D1，E、F、G、H分别为AB、AD、C1B1、C1D1的中点，试判断下列直线是否平行．
(1)AD1与BC1；
(2)EF与GH；
(3)DE与HB1．
答案：
解析：
解析：
|
解：(1)AD1与BC1平行．∵AB (2)EF与GH平行．∵EF∥BD∥B1D1∥GH． (3)DE与HB1平行．取CD中点为S，连结BS，如图，可证DE∥BS∥HB1．
|
D1C1，∵ABC1D1是平行四边形，∴AD1∥BC1．
练习册系列答案
相关题目
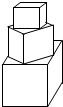有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点．已知最底层正方体的棱长为2，且该塔形的表面积（含最底层正方体的底面面积）超过39，则该塔形中正方体的个数至少是（ ）| A、4 | B、5 | C、6 | D、7 |
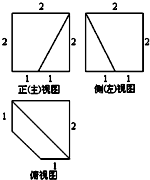已知一个棱长为2的正方体，被一个平面截后所得几何体的三视图如图所示，则该几何体的体积是（ ）| A、8 | ||
B、
| ||
C、
| ||
D、
|
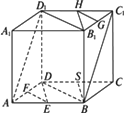
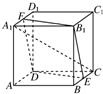
如图所示，已知正方体ABCD-A1B1C1D1的棱长为a，E，F分别是BC，A1D1的中点．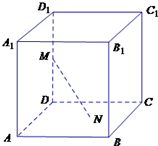
如图所示，已知正方体ABCD-A1B1C1D1的棱长为2，长为2的线段MN的一个端点M在棱DD1上运动，另一端点N在正方形ABCD内运动，则MN的中点的轨迹的面积为（ ）