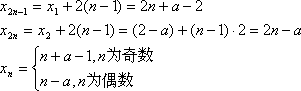题目内容
已知点B1(1，y1)，B2(2，y2)，…，Bn(n，yn)，…(n∈N)顺次为直线
上的点，点A1(x1，0)，A2(x2，0)，…，An(xn，0)顺次为x轴上的点，其中x1＝a(0＜a＜1)．对于任意自然数n，点An，Bn，An＋1构成以Bn为顶点的等腰三角形．
(1)求数列{yn}的通项公式，并证明它为等差数列；
(2)求证：xn+2－xn是常数，并求数列{xn}的通项公式；
(3)上述等腰△AnBnAn+1中是否可能存在直角三角形，若可能，求出此时a的值；若不可能，请说明理由．
答案：
解析：
解析：
|
(1) (2)由题意得 ∴ (3)当n为奇数时， 当n为偶数时， 作 要使等腰三角形为直角三角形，则 10n为奇数， 当 20n为偶数， 综上 |
为定值
成等差数列
成等差数列
，无解
时，存在直角三角形
练习册系列答案
相关题目
x+
上的点，点A1(x1，0)，A2(x2，0)，…，An(xn，0)，…顺次为x轴上的点，其中x1=a(0＜a＜1).对于任意n∈N*，点An，Bn，An+1构成以Bn为顶点的等腰三角形．
上的点，点A1(x1，0)，A2(x2，0)，…，An(xn，0)顺次为x轴上的点，其中x1＝a(0＜a＜1)．对于任意自然数n，点An，Bn，An＋1构成以Bn为顶点的等腰三角形．
上的点，点A1(x1，0)，A2(x2，0)，…An(xn，0)，…(n∈N*)顺次为
轴上的点，其中x1＝a(0＜a＜1)，对任意的n∈N*，点An、Bn、An+1构成以Bn为顶点的等腰三角形．
,试问在△AnBnAn+1(n∈N*)中是否存在直角三角形?若存在，求出a的值；若不存在，请说明理由.
ax3
x2+cx+d(a、c、d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2-bx+
,解不等式f′(x)+h(x)＜0.