题目内容
已知常数c、d都是实数,在数列{an}与{bn}中,a1=0,b1=1.对任何正整数n,等式an+1=can+d,bn+1=cbn+d都成立.(1)当c=1时,求数列{an}与{bn}的通项公式;
(2)当c>0且c≠1时,要使数列{bn}是公比不为1的等比数列,求d的值;
(3)当c>0时,设数列{an}的前n项和、{bn}的前n项和分别为Sn与Tn,求(T1+T2+…+T100)-(S1+S2+…+S100)的值.
解:(1)∵c=1>0,∴an=c·an-1+d=an-1+d,bn=bn-1+d(n≥2).
∴{an}、{bn}都是公差为d的等差数列.∵a1=0,b1=1,∴an=(n-1)d,bn=1+(n-1)d(n∈N*).
(2)∵c>0,∴bn=cbn-1+d.∴![]() =c+
=c+![]() .∵{bn}是等比数列,∴
.∵{bn}是等比数列,∴![]() 为常数.
为常数.
∵{bn}是公比不为1的等比数列,∴bn-1不是常数.∴必有d=0.
(3)∵c>0,∴an=c·an-1+d,bn=c·bn-1+d.两式相减得:bn-an=c(bn-1-an-1)(n≥2),
∴{bn-an}为等比数列.∴bn-an=(b1-a1)cn-1=cn-1.
∴Tn-Sn=(b1-a1)+(b2-a2)+…+(bn-an)=1+c+c2+…+cn-1=n,c=1,
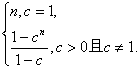 ,c>0且c≠1.
,c>0且c≠1.
∴当c=1时,(T1+T2+…+T100)-(S1+S2+…+S100)
=(T1-S1)+(T2-S2)+…+(T100-S100)
=1+2+3+…+100=![]() =5 050.
=5 050.
∴当c>0且c≠1时,(T1+T2+…+T100)-(S1+S2+…+S100)
=(T1-S1)+(T2-S2)+…+(T100-S100)
=![]() +
+![]() +…+
+…+![]() =
=![]() [100
[100![]() ]=
]=![]() .
.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目