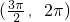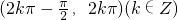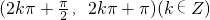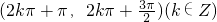Question

使函数y=sinx递减且函数y=cosx递增的区间是（　　）

• A、(

  3π

  2

  ，2π)
• B、(2kπ-

  π

  2

  ，2kπ)(k∈Z)
• C、(2kπ+

  π

  2

  ，2kπ+π)(k∈Z)
• D、(2kπ+π，2kπ+

  3π

  2

  )(k∈Z)

Answer 1

分析：先求出正弦函数的减区间和余弦函数的增区间，即可分别判断出y=sinx与y=cosx在A，B，C，D区间上的单调性，进而可确定答案．

解答：解：y=sinx的单调递减区间是[

π

2

+2kπ，

3π

2

+2kπ]，k∈Z
y=cosx的递增区间是[π+2kπ，2π+2kπ]，k∈Z，
∴在区间(

3π

2

，2π)上y=sinx单调递增，A不符合要求．
在区间(2kπ-

π

2

，2kπ)上y=sinx单调递增，B不符合要求；
在区间(2kπ+

π

2

，2kπ+π)上y=cosx单调递减，C不符合要求；
在区间(2kπ+π，2kπ+

3π

2

)上y=sinx递减，y=cosx为递增函数，故D符合要求．
故选D．

点评：本题主要考查正弦函数、余弦函数的单调性．三角函数的基本性质是高考的重点对象，一般以基础题为主，要求考生平时要注意基础知识的积累．