��Ŀ����
 ij��λ��֯Ⱥ���Ե�ɽ���������ļ��N��ʦ��־Ը�ߣ�������־Ը���ְ����������Ϊ15-20��20-25��25-30��30-35��35-40��40-45��������Σ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����֪30-35֮���־Ը�߹�8�ˣ�
ij��λ��֯Ⱥ���Ե�ɽ���������ļ��N��ʦ��־Ը�ߣ�������־Ը���ְ����������Ϊ15-20��20-25��25-30��30-35��35-40��40-45��������Σ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����֪30-35֮���־Ը�߹�8�ˣ�
��1����N��20-B.30֮���־Ը������N1��
��2����֪20-2B.5��30-35֮�����2��Ӣ���ʦ���ִ���������θ�ѡȡ2�˵��νӴ��������������ѡ��Ӱ�죬������ѡ������ѡ�ж�������1��Ӣ���ʦ�ĸ����Ƕ��٣�
��3����֯�ߴ�35-45֮���־Ը�ߣ����й���4��Ů��ʦ������ȫΪ�н�ʦ�������ѡȡ3�����κ��ڱ��Ϲ����������н�ʦ������ΪX����X�ĸ��ʷֲ��к;�ֵ��
�⣺��1��30-35֮���Ƶ��Ϊ0.04��5=0.2������30-35֮���־Ը�߹�8�ˣ���N= =40��
=40��
20-30֮���Ƶ��Ϊ1-��0.01+0.04+0.02+0.01����5=0.6����N1=0.6��40=24
��2���ɣ�1��֪��20-25֮���־Ը�߹���12�ˣ�30-35֮���־Ը�߹�8��
�衰��ѡ������ѡ�ж�������1��Ӣ����ʦ��Ϊ�¼�A����P��A��= ?
? =
=
��3��������֪��Ů��ʦ��4�����н�ʦ��2���� X=0��1��2
P��X=0��= ��P��X=1��=
��P��X=1��= ��P��X=2��=
��P��X=2��=
���Էֲ���Ϊ
��ֵΪ0��? +1��?
+1��? +2��?
+2��? =1��
=1��
��������1������ֱ��ͼ���ɵ�30-35֮���Ƶ��Ϊ0.04��5=0.2������30-35֮���־Ը�߹�8�ˣ�����N��20-30֮���Ƶ��Ϊ1-��0.01+0.04+0.02+0.01����5=0.6���ʿ���N1��ֵ��
��2���ɣ�1��֪��20-25֮���־Ը�߹���12�ˣ�30-35֮���־Ը�߹�8�ˣ��ɴ˿�����ѡ������ѡ�ж�������1��Ӣ����ʦ�ĸ��ʣ�
��3��������֪��Ů��ʦ��4�����н�ʦ��2�����ʿɵ�X��ȡֵ���������ʣ����ɵõ�X�ĸ��ʷֲ��к;�ֵ��
���������⿼��Ƶ��ֱ��ͼ��������ɢ����������ķֲ������ֵ������Ĺؼ���ȷ��������ȡֵ�뺬�壮
 =40��
=40�� 20-30֮���Ƶ��Ϊ1-��0.01+0.04+0.02+0.01����5=0.6����N1=0.6��40=24
��2���ɣ�1��֪��20-25֮���־Ը�߹���12�ˣ�30-35֮���־Ը�߹�8��
�衰��ѡ������ѡ�ж�������1��Ӣ����ʦ��Ϊ�¼�A����P��A��=
 ?
? =
=
��3��������֪��Ů��ʦ��4�����н�ʦ��2���� X=0��1��2
P��X=0��=
 ��P��X=1��=
��P��X=1��= ��P��X=2��=
��P��X=2��=
���Էֲ���Ϊ
| X | 0 | 1 | 2 |
| P |  |  |  |
 +1��?
+1��? +2��?
+2��? =1��
=1����������1������ֱ��ͼ���ɵ�30-35֮���Ƶ��Ϊ0.04��5=0.2������30-35֮���־Ը�߹�8�ˣ�����N��20-30֮���Ƶ��Ϊ1-��0.01+0.04+0.02+0.01����5=0.6���ʿ���N1��ֵ��
��2���ɣ�1��֪��20-25֮���־Ը�߹���12�ˣ�30-35֮���־Ը�߹�8�ˣ��ɴ˿�����ѡ������ѡ�ж�������1��Ӣ����ʦ�ĸ��ʣ�
��3��������֪��Ů��ʦ��4�����н�ʦ��2�����ʿɵ�X��ȡֵ���������ʣ����ɵõ�X�ĸ��ʷֲ��к;�ֵ��
���������⿼��Ƶ��ֱ��ͼ��������ɢ����������ķֲ������ֵ������Ĺؼ���ȷ��������ȡֵ�뺬�壮

��ϰ��ϵ�д�
�����Ŀ
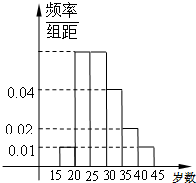 ij��λ��֯Ⱥ���Ե�ɽ���������ļ��N��ʦ��־Ը�ߣ�������־Ը���ְ����������Ϊ15-20��20-25��25-30��30-35��35-40��40-45��������Σ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����֪30-35֮���־Ը�߹�8�ˣ�
ij��λ��֯Ⱥ���Ե�ɽ���������ļ��N��ʦ��־Ը�ߣ�������־Ը���ְ����������Ϊ15-20��20-25��25-30��30-35��35-40��40-45��������Σ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����֪30-35֮���־Ը�߹�8�ˣ�