题目内容
函数f(x)=k•a-x(k,a为常数,a>0且a≠1)的图象过点A(0,1),B(3,8).(1)求函数f(x)的解析式;
(2)若函数
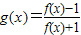 ,试判断函数g(x)的奇偶性.
,试判断函数g(x)的奇偶性.
【答案】分析:(1)将A(0,1),B(3,8)代入函数解析式,得到关于k和a的方程,解方程即可得k和a的值,最后写出解析式即可
(2)先判断函数的定义域是否关于原点对称,再证明g(-x)=-g(x),由奇函数的定义可判断函数g(x)的奇偶性
解答:解:(1)将A(0,1),B(3,8)代入函数解析式,得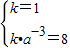 ,
,
∴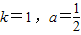 ,
,
∴f(x)=2x
(2)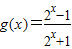 ,其定义域为R,
,其定义域为R,
又
∴函数g(x)为奇函数.
点评:本题考查了函数解析式的求法,函数奇偶性的判断方法,属基础题,解题时要认真运算,在证明奇偶性时还要注意代数变形方法
(2)先判断函数的定义域是否关于原点对称,再证明g(-x)=-g(x),由奇函数的定义可判断函数g(x)的奇偶性
解答:解:(1)将A(0,1),B(3,8)代入函数解析式,得
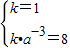 ,
,∴
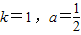 ,
,∴f(x)=2x
(2)
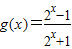 ,其定义域为R,
,其定义域为R,又

∴函数g(x)为奇函数.
点评:本题考查了函数解析式的求法,函数奇偶性的判断方法,属基础题,解题时要认真运算,在证明奇偶性时还要注意代数变形方法

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
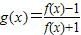 ,试判断函数g(x)的奇偶性,并说明理由.
,试判断函数g(x)的奇偶性,并说明理由.