题目内容
已知一圆的圆心为（2，-3），一条直径的端点分别在x轴和y轴上，则此圆的方程是（ ）A．（x-2）2+（y+3）2=13
B．（x+2）2+（y-3）2=13
C．（x-2）2+（y+3）2=52
D．（x+2）2+（y-3）2=52
【答案】分析：直径的两个端点分别A（a，0）B（0，b），圆心（2，-3）为AB的中点，利用中点坐标公式求出a，b后，再利用两点距离公式求出半径．
解答：解：设直径的两个端点分别A（a，0）B（0，b）．圆心为点（2，-3），由中点坐标公式得，a=4，b=-6，∴r=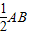
=
，
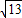则此圆的方程是 （x-2）2+（y+3）2=13，
故选A．
点评：本题考查圆的方程求解，确定圆心、半径即能求出圆的标准方程．
解答：解：设直径的两个端点分别A（a，0）B（0，b）．圆心为点（2，-3），由中点坐标公式得，a=4，b=-6，∴r=
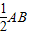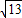=，则此圆的方程是 （x-2）2+（y+3）2=13，
故选A．
点评：本题考查圆的方程求解，确定圆心、半径即能求出圆的标准方程．
练习册系列答案
津桥教育计算小状元系列答案
相关题目