题目内容
(1)若2a=5b=10,求
+
的值;
(2)已知x
+x-
=3,求
的值.
| 1 |
| a |
| 1 |
| b |
(2)已知x
| 1 |
| 2 |
| 1 |
| 2 |
| x2+x-2-2 |
| x+x-1-3 |
分析:(1)要求
+
的值需求出a,b的值故可根据条件2a=5b=10结合指数式与对数式的转化公式:ab=N?b=logaN求出a,b然后代入再结合换底公式化简即可得解.
(2)通过已知表达式求出x+x-1,x2+x-2的值,然后求解所求表达式的值即可.
| 1 |
| a |
| 1 |
| b |
(2)通过已知表达式求出x+x-1,x2+x-2的值,然后求解所求表达式的值即可.
解答:解:(1)∵2a=5b=10
∴a=log210,b=log510
∴
+
=
+
=log102+log105=log1010=1.
(2)因为x
+x-
=3,所以(x
+x-
)2=9,
∴x+2+x-1=9,
∴x+x-1=7,
∴(x+x-1)2=49,
∴x2+x-2=47
∴
=
.
∴a=log210,b=log510
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| log210 |
| 1 |
| log510 |
(2)因为x
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴x+2+x-1=9,
∴x+x-1=7,
∴(x+x-1)2=49,
∴x2+x-2=47
∴
| x2+x-2-2 |
| x+x-1-3 |
| 47-2 |
| 7-3 |
| 45 |
| 4 |
点评:本题主要考察指数式与对数式的互化.解题的关键是熟记指数式与对数式的转化公式:ab=N?b=logaN和对数的换底公式;有理指数幂的运算,考查计算能力.

练习册系列答案
相关题目
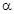 是第一象限角,那么
是第一象限角,那么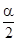 是第一或第三象限角
是第一或第三象限角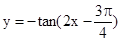 的单调递减区间是
的单调递减区间是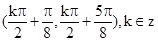
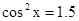 可能成立
可能成立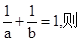 m=1
m=1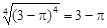 必定成立
必定成立 的值;
的值;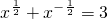 ,求
,求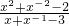 的值.
的值.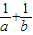 的值;
的值;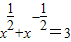 ,求
,求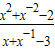 的值.
的值.