题目内容
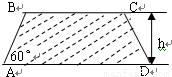
建造一条防洪堤,其断面为等腰梯形,腰与底边成角为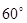 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为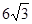 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段 与两腰长的和)要最小.
与两腰长的和)要最小.
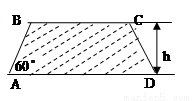
(1)求外周长的最小值,并求外周长最小时防洪堤高h为多少米?
(2)如防洪堤的高限制在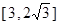 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米?
【答案】
(1)外周长的最小值为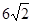 米,此时堤高
米,此时堤高 为
为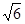 米.
米.
(2)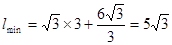 (米).(当
(米).(当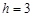 时取得最小值)
时取得最小值)
【解析】
试题分析:(1)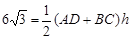 ,AD=BC+2×
,AD=BC+2×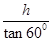 =BC+
=BC+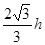 ,
, 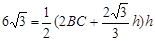 ,
,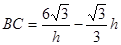 .
.
设外周长为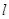 ,则
,则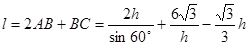 ,
,
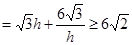
当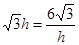 ,即
,即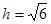 时等号成立.外周长的最小值为
时等号成立.外周长的最小值为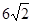 米,此时堤高
米,此时堤高 为
为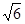 米.
米.
(2)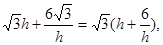 设
设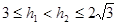 ,则
,则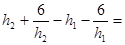
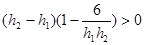 ,
,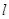 是
是 的增函数,
的增函数,
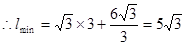 (米).(当
(米).(当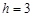 时取得最小值)
时取得最小值)
考点:本题主要考查函数模型,求函数最值。
点评:中档题,利用图象特征,确定得到周长的表达式,在进一步求函数最值过程中,可以应用导数,也可以运用均值定理,应用均值定理时,要注意“一正、二定、三相等”缺一不可。

练习册系列答案
相关题目
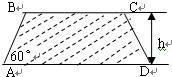 建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为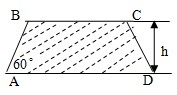 (2008•杨浦区二模)建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(2008•杨浦区二模)建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为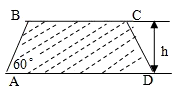 建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为 平 方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段BC与两腰长的和)要最小.
平 方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段BC与两腰长的和)要最小.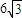 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段BC与两腰长的和)要最小.
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段BC与两腰长的和)要最小.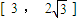 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米?