题目内容
给出下列四个结论:①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
②“若am2<bm2,则a<b”的逆命题为真;
③已知空间直线m,n,l,则m∥n的一个必要非充分条件是m,n与l所成角相等;
④已知函数
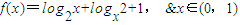 ,则f(x)的最大值为-1.
,则f(x)的最大值为-1.其中正确结论的序号是 .
【答案】分析:①由特称命题“?x∈M,p(x)”的否定形式为全称命题“?x∈M,¬p(x)”,可判断其真假;
②由逆命题概念及不等式的性质,可判断其真假;
③由空间直线夹角的概念及两直线平行的性质、判定,想象空间图形判断其真假;
④由对数性质及基本不等式,可判断其真假.
解答:解:①特称命题“?x∈R,x2-x>0”的否定是全称命题“?x∈R,x2-x≤0”,所以①正确;
②命题“若am2<bm2,则a<b”的逆命题为“若a<b,则am2<bm2”,显然若m=0结论不成立,所以②错误;
③已知空间直线m,n,l:若m,n与l所成角相等,未必有m∥n;若m∥n,则m,n与l所成角相等.
所以“已知空间直线m,n,l,则m∥n的一个必要非充分条件是m,n与l所成角相等.”是正确的,所以③正确;
④当x∈(0,1)时,log2x<0,所以f(x)=log2x+logx2+1=log2x+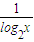 +1≤-2+1=-1,显然当x=
+1≤-2+1=-1,显然当x= 时,f(x)取得最大值.
时,f(x)取得最大值.
所以④正确.
故答案为①③④.
点评:此类问题是对已学数学知识的多点考查,其考查面较广,但基础性强,每一问的难度都不大,属于基础题范畴.
②由逆命题概念及不等式的性质,可判断其真假;
③由空间直线夹角的概念及两直线平行的性质、判定,想象空间图形判断其真假;
④由对数性质及基本不等式,可判断其真假.
解答:解:①特称命题“?x∈R,x2-x>0”的否定是全称命题“?x∈R,x2-x≤0”,所以①正确;
②命题“若am2<bm2,则a<b”的逆命题为“若a<b,则am2<bm2”,显然若m=0结论不成立,所以②错误;
③已知空间直线m,n,l:若m,n与l所成角相等,未必有m∥n;若m∥n,则m,n与l所成角相等.
所以“已知空间直线m,n,l,则m∥n的一个必要非充分条件是m,n与l所成角相等.”是正确的,所以③正确;
④当x∈(0,1)时,log2x<0,所以f(x)=log2x+logx2+1=log2x+
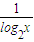 +1≤-2+1=-1,显然当x=
+1≤-2+1=-1,显然当x= 时,f(x)取得最大值.
时,f(x)取得最大值.所以④正确.
故答案为①③④.
点评:此类问题是对已学数学知识的多点考查,其考查面较广,但基础性强,每一问的难度都不大,属于基础题范畴.

练习册系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=