题目内容
已知直线方程为ax+by+c=0,当a<0,b>0,c>0时,该直线经过( )
分析:求出直线与x轴、y轴的交点坐标分别为A(-
,0)、B(0,-
),根据题意得点A在x轴的正半轴上且点B在y轴的负半轴上,由此即可得到直线经过的象限.
| c |
| a |
| c |
| b |
解答:解:对直线令y=0得x=-
; 再令x=0得y=-
∴直线交x轴于点A(-
,0),交y轴于点B(0,-
)
∵a<0,b>0,c>0
∴-
为正数且-
为负数,
即点A(-
,0)在x轴的正半轴上,且点B(0,-
)在y轴的负半轴上
由此可得直线一定经过一、三、四象限,
故选:D
| c |
| a |
| c |
| b |
∴直线交x轴于点A(-
| c |
| a |
| c |
| b |
∵a<0,b>0,c>0
∴-
| c |
| a |
| c |
| b |
即点A(-
| c |
| a |
| c |
| b |
由此可得直线一定经过一、三、四象限,
故选:D
点评:本题给出含有字母参数的直线方程,在已知参数的正负情况下求直线经过的象限.着重考查了直线的基本量与基本形式的知识,属于中档题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
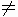 0),试写出求直线在x轴上的截距,在y轴上的截距以及斜率的算法.
0),试写出求直线在x轴上的截距,在y轴上的截距以及斜率的算法.