题目内容
已知数列{an}中a1=2,前n项的和为Sn,且4tSn+1-(3t+8)Sn=8t,其中t<-3,n∈N*;(1)证明数列{an}为等比数列;
(2)判定{an}的单调性,并证明.
【答案】分析:(1)由4tSn+1-(3t+8)Sn=8t按照通项与前n项和间的关系,分当n=1和n≥2两种情况探求得4tan+1-(3t+8)an=0,进而变形得 (n≥2,∴t<-3)由等比数列的定义判断.
(n≥2,∴t<-3)由等比数列的定义判断.
(2)因为是正项数列,可用作商比较法 <1得到{an}为递减数列.
<1得到{an}为递减数列.
解答:解(1)证明:∵4tSn+1-(3t+8)Sn=8t①
当n=1时,4t(a1+a2)-(3t+8)a1=8t而a1=2 (2分)
(2分)
又∵4tSn-(3t+8)Sn-1=8t②(n≥2)
由①②得4tan+1-(3t+8)an=0
即 (n≥2,∴t<-3)(4分)
(n≥2,∴t<-3)(4分)
而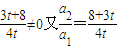
∴{an}是等比数列(8分)
(2)∵an=2( >0(∵t<-3)
>0(∵t<-3) (12分)
(12分)
∵t<-3∴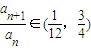 (14分)
(14分)
则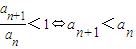
∴{an}为递减数列(16分)
点评:本题主要考查数列的通项与前n项和之间的关系和判断数列的方法,一般用定义或通项公式,证明数列是单调数列时往往用比较法.
 (n≥2,∴t<-3)由等比数列的定义判断.
(n≥2,∴t<-3)由等比数列的定义判断.(2)因为是正项数列,可用作商比较法
 <1得到{an}为递减数列.
<1得到{an}为递减数列.解答:解(1)证明:∵4tSn+1-(3t+8)Sn=8t①
当n=1时,4t(a1+a2)-(3t+8)a1=8t而a1=2
 (2分)
(2分)又∵4tSn-(3t+8)Sn-1=8t②(n≥2)
由①②得4tan+1-(3t+8)an=0
即
 (n≥2,∴t<-3)(4分)
(n≥2,∴t<-3)(4分)而
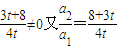
∴{an}是等比数列(8分)
(2)∵an=2(
 >0(∵t<-3)
>0(∵t<-3) (12分)
(12分)∵t<-3∴
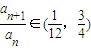 (14分)
(14分)则
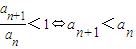
∴{an}为递减数列(16分)
点评:本题主要考查数列的通项与前n项和之间的关系和判断数列的方法,一般用定义或通项公式,证明数列是单调数列时往往用比较法.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目