题目内容
二面角α-l-β的平面角记为θ,P为空间的任意一点,P到平面α、β的距离分别为A.75° B.165° C.75°或165° D.以上答案均错
C
解析:本题主要考查了垂面法求二面角的平面角的方法.注意点P可能在二面角内部,也可能在二面角的外部.如图.
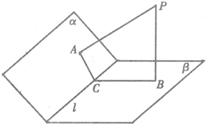
PA⊥α,PB⊥β,垂足分别为A、B.所以PA=![]() ,PB=1,设PA、PB确定的平面交α、β分别于AC、BC,PA⊥α,PB⊥β,α∩β=l,∴PA⊥l,PB⊥l,PA∩PB=l,∴l⊥平面PACB,得PC⊥l,l⊥BC,l⊥AC,PC即为点P到l的距离,所以PC=2.∠ACB即为二面角α-l-β的平面角θ.在Rt△PAC中可得∠ACP=45°,在Rt△PBC中可得∠BCP=30°,所以θ=∠ACB=75°.同理,当点P在二面角外部时,可得θ=∠ACB=105°.所以θ=75°或105°.
,PB=1,设PA、PB确定的平面交α、β分别于AC、BC,PA⊥α,PB⊥β,α∩β=l,∴PA⊥l,PB⊥l,PA∩PB=l,∴l⊥平面PACB,得PC⊥l,l⊥BC,l⊥AC,PC即为点P到l的距离,所以PC=2.∠ACB即为二面角α-l-β的平面角θ.在Rt△PAC中可得∠ACP=45°,在Rt△PBC中可得∠BCP=30°,所以θ=∠ACB=75°.同理,当点P在二面角外部时,可得θ=∠ACB=105°.所以θ=75°或105°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
