题目内容
已知圆F的方程是x2+y2-2y=0,抛物线的顶点在原点,焦点是圆心F,过F引倾斜角为α的直线l,l与抛物线和圆依次交于A、B、C、D四点(在直线l上,这四个点从左至右依次为A、B、C、D),若|AB|,|BC|,|CD|成等差数列,则α的值为( )
A、±arctan
| ||||||||
B、
| ||||||||
C、arctan
| ||||||||
D、arctan
|
分析:根据抛物线的焦点是圆心F,求出p,进而求出抛物线的解析式;据|AB|,|BC|,|CD|成等差数列,求出AD的长度,A、D两点是抛物线和直线的交点,联立抛物线和直线,利用两点间距离公式即可求出结果.
解答:解:∵圆Fx2+y2-2y=0 即x2+(y-1)2=1
∴F(0,1),r=1
∵抛物线以F点为焦点
=1
∴抛物线方程为:x2=4y
过F点的直线与抛物线相交于A、D两点,
BC为圆F的直径|BC|=2
∵|AB|,|BC|,|CD|成等差数列
∴2|BC|=|AB|+|CD|=|AD|-|BC|=|=|AD|-2=4
∴|AD|=6
∵直线l过F(0,1)则设直线解析式为:y=kx+1
A、D两点是过F点的直线与抛物线交点
设A(x1,y1)D(x2,y2)则|AD|=
=6
联立y=kx+1和x2=4y,得x2-4kx-4=0
∴x1x2=-4 x1+x2=4k
∴|AD|=
=
=
=
=
=6
∴1+k2=
∴k=±
∴α的值为:arctan
或π-arctan
故选D.
∴F(0,1),r=1
∵抛物线以F点为焦点
| p |
| 2 |
∴抛物线方程为:x2=4y
过F点的直线与抛物线相交于A、D两点,
BC为圆F的直径|BC|=2
∵|AB|,|BC|,|CD|成等差数列
∴2|BC|=|AB|+|CD|=|AD|-|BC|=|=|AD|-2=4
∴|AD|=6
∵直线l过F(0,1)则设直线解析式为:y=kx+1
A、D两点是过F点的直线与抛物线交点
设A(x1,y1)D(x2,y2)则|AD|=
| (x1-x2)2+(y1-y2)2 |
联立y=kx+1和x2=4y,得x2-4kx-4=0
∴x1x2=-4 x1+x2=4k
∴|AD|=
| (x1-x2)2+(y1-y2)2 |
| (x1-x2) 2+k2(x1-x2) 2 |
| (x1-x2) 2(1+k2) |
| [(x1+x2) 2- 4x1x2](1+k2) |
| 16(1+k2)2 |
∴1+k2=
| 3 |
| 2 |
∴k=±
| ||
| 2 |
∴α的值为:arctan
| ||
| 2 |
| ||
| 2 |
故选D.
点评:本题主要综合考查直线与圆、抛物线以及数列的相关知识,关键是利用两点间的距离公式;同时注意运用数形结合的方法解决此类问题.

练习册系列答案
相关题目



 或π-arctan
或π-arctan
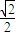
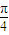

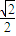 或π-arctan
或π-arctan