题目内容
已知P是直线 上的动点,PA、PB是圆
上的动点,PA、PB是圆 的两条切线,C是圆心,那么四边形PACB面积的最小值( )
的两条切线,C是圆心,那么四边形PACB面积的最小值( )
A. B.2
B.2 C.
C. D.2
D.2
 上的动点,PA、PB是圆
上的动点,PA、PB是圆 的两条切线,C是圆心,那么四边形PACB面积的最小值( )
的两条切线,C是圆心,那么四边形PACB面积的最小值( )A.
 B.2
B.2 C.
C. D.2
D.2
C
试题分析:如图
 ,所以四边形PACB面积的最小值就是
,所以四边形PACB面积的最小值就是 的最小值,而
的最小值,而 ,本题要求出最小的
,本题要求出最小的 的值,即为圆心C(1,1)到直线
的值,即为圆心C(1,1)到直线 的最短距离
的最短距离 ,所以
,所以 .即四边形PACB面积的最小值是
.即四边形PACB面积的最小值是 .所以选C.
.所以选C.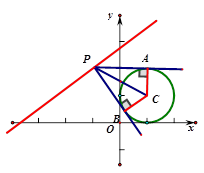

练习册系列答案
相关题目
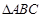 的三个顶点
的三个顶点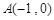 ,
,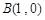 ,
,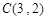 ,其外接圆为
,其外接圆为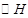 .
.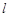 过点
过点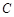 ,且被
,且被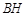 上的任意一点
上的任意一点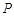 ,若在以
,若在以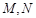 ,使得点
,使得点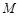 是线段
是线段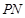 的中点,求
的中点,求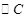 的半径
的半径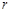 的取值范围.
的取值范围. ,直线
,直线 .
. 与圆C的位置关系;
与圆C的位置关系;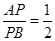 ,求此时直线
,求此时直线
 直线
直线
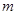 取何实数,直线
取何实数,直线 与圆C恒相交;
与圆C恒相交;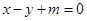 与圆
与圆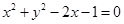 有两个不同交点的一个充分不必要条件是( )
有两个不同交点的一个充分不必要条件是( )



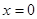 绕点
绕点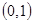 按逆时针方向旋转
按逆时针方向旋转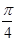 后所得直线与圆
后所得直线与圆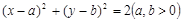 相切,,则
相切,,则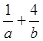 的最小值为( )
的最小值为( )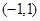 的直线与圆
的直线与圆 截得的弦长为
截得的弦长为 ,则该直线的方程为 .
,则该直线的方程为 . (
( 为参数)与圆
为参数)与圆 (
( 为参数),则直线
为参数),则直线 的倾斜角及圆心
的倾斜角及圆心 的直角坐标分别是
的直角坐标分别是