题目内容
已知圆C过两点M(2,2),N(1,3),且圆心C在直线3x-y-3=0上,点A(3,5)
(1)求圆C的方程;
(2)求过点A的圆C的切线方程;
(3)O点是坐标原点,连结OA,OC,求△AOC的面积S.
(1)求圆C的方程;
(2)求过点A的圆C的切线方程;
(3)O点是坐标原点,连结OA,OC,求△AOC的面积S.
分析:(1)由题意可求MN的垂直平分线得方程,联立已知直线可得圆心C的坐标,由距离公式可得MC,即圆的比较,由圆的标准方程可得;
(2)设直线方程为y-5=k(x-3),由圆心到直线的距离等于半径可得k值,可得直线,验证直线无斜率的情形可得;
(3)由距离公式可得|AO|,可得点C到直线OA的距离d,代入面积公式可得.
(2)设直线方程为y-5=k(x-3),由圆心到直线的距离等于半径可得k值,可得直线,验证直线无斜率的情形可得;
(3)由距离公式可得|AO|,可得点C到直线OA的距离d,代入面积公式可得.
解答:解:(1)由中点坐标公式可得MN的中点为(
,
),
MN的斜率为
=-1,∴MN的垂直平分线的斜率为1,
故MN的垂直平分线为y-
=x-
,即y=x+1,
联立
解得x=2,y=3,即圆心C(2,3),
由距离公式可得MC2=(2-2)2+(3-2)2=1,
∴圆C的方程为:(x-2)2+(y-3)2=1
(2)当切线的斜率不存在时,过点A的直线方程为x=3,
圆心C(2,3)到直线的距离为1,满足条件.
当斜率存在时,设直线方程为y-5=k(x-3),即kx-y+5-3k=0,
由直线与圆相切得
=1,∴k=
.
∴直线方程为x=3或y=
x+
,即x=3,或3x-4y+11=0
(3)由距离公式可得|AO|=
=
,
直线OA的方程为5x-3y=0,
∴点C到直线OA的距离d=
,
∴△AOC的面积S=
d|AO|=
| 3 |
| 2 |
| 5 |
| 2 |
MN的斜率为
| 2-3 |
| 2-1 |
故MN的垂直平分线为y-
| 5 |
| 2 |
| 3 |
| 2 |
联立
|
由距离公式可得MC2=(2-2)2+(3-2)2=1,
∴圆C的方程为:(x-2)2+(y-3)2=1
(2)当切线的斜率不存在时,过点A的直线方程为x=3,
圆心C(2,3)到直线的距离为1,满足条件.
当斜率存在时,设直线方程为y-5=k(x-3),即kx-y+5-3k=0,
由直线与圆相切得
| |-k+2| | ||
|
| 3 |
| 4 |
∴直线方程为x=3或y=
| 3 |
| 4 |
| 11 |
| 4 |
(3)由距离公式可得|AO|=
| 9+25 |
| 34 |
直线OA的方程为5x-3y=0,
∴点C到直线OA的距离d=
| 1 | ||
|
∴△AOC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查圆的方程的求解以及圆的切线方程,涉及分类讨论的思想,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
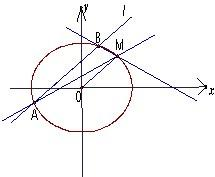 如图,已知椭圆C过点M(2,1),两个焦点分别为
如图,已知椭圆C过点M(2,1),两个焦点分别为