Question

【题目】设椭圆C： =1（a＞b＞0）的焦点F1 ， F2 ， 过右焦点F2的直线l与C相交于P、Q两点，若△PQF1的周长为短轴长的2 倍．
（Ⅰ）求C的离心率；
（Ⅱ）设l的斜率为1，在C上是否存在一点M，使得 ？若存在，求出点M的坐标；若不存在，说明理由．

Answer 1

【答案】解：（Ⅰ）∵椭圆C： =1（a＞b＞0）的焦点F1，F2，过右焦点F2的直线l与C相交于P、Q两点，

△PQF1的周长为短轴长的2 倍，△PQF1的周长为4a

∴依题意知 ，即

∴C的离心率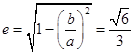

（Ⅱ）设椭圆方程为 ，直线的方程为y=x﹣c，

代入椭圆方程得

设P（x1，y1），Q（x2，y2），则 ，

设M（x0，y0），则 ①

由 得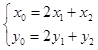

代入①得

因为 ， ，

所以 ②

而

从而②式不成立．

故不存在点M，使 成立

【解析】（Ⅰ）由椭圆的焦点F1，F2，过右焦点F2的直线l与C相交于P、Q两点，△PQF1的周长为短轴长的2 倍，得到 ，由此能求出椭圆C的离心率．（Ⅱ）设椭圆方程为 ，直线的方程为y=x﹣c，代入椭圆方程得 ，由此利用韦达定理、椭圆性质、向量知识，结合已知条件能求出不存在点M，使 成立．