题目内容
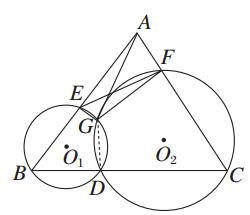
如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.
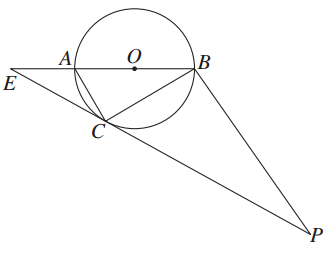
(1)求证:BC2=AC·BP;
(2)若EC=2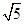 ,求PB的长.
,求PB的长.

(1)求证:BC2=AC·BP;
(2)若EC=2
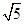 ,求PB的长.
,求PB的长.(1)见解析 (2)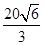
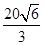
解:(1)∵AB为圆O的直径,∴∠ACB=90°.
又AC∥BP,∴∠ACB=∠CBP,∠ECA=∠P.
∵EC为圆O的切线,∴∠ECA=∠ABC,∴∠ABC=∠P,
∴△ACB∽△CBP.
∴
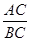 =
=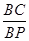 ,即BC2=AC·BP.
,即BC2=AC·BP.(2)∵EC为圆O的切线,EC=2
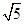 ,AB=8,
,AB=8,∴EC2=EA·EB=EA(EA+AB),∴EA=2.
∵∠ECA=∠ABC,∴△ACE∽△CBE,∴
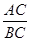 =
=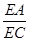 =
=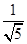 .
.∵AB为圆O的直径,∴∠ACB=90°,∴AC2+BC2=AB2.
∴AC=
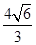 ,由
,由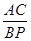 =
=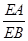 ,可得PB=
,可得PB=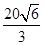 .
.
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 与圆
与圆 分别交于A,B两点.若
分别交于A,B两点.若 ,则实数
,则实数 的值为( ).
的值为( ).


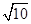 .
.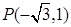 的直线
的直线 与圆
与圆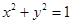 有公共点,则直线
有公共点,则直线


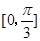





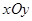 中,点
中,点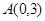 ,直线
,直线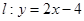 .设圆
.设圆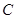 的半径为
的半径为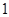 ,圆心在
,圆心在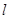 上.
上.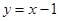 上,过点
上,过点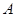 作圆
作圆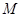 ,使
,使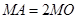 ,求圆心
,求圆心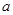 的取值范围.
的取值范围.