题目内容

图3-4-3所示的平面直角坐标系中，在y轴正半轴（坐标原点除外）上给定两点A、B，试在x轴的正半轴（坐标原点除外）上求一点C，使∠ACB取得最大值.

思路分析：本题是一个含有识图以及与三角函数有关的综合题，首先根据图形建立∠ACB某一三角函数的一个解析式，根据解析式和均值不等式求最值即可.

解：设点A坐标为（0，a），点B坐标为（0，b），0＜b＜a，点C坐标为（x，0）（x＞0），∠ACB=α，∠OCB=β，则∠OCA=α+β（0＜α＜），

∴tanα=tan［（α+β）－β］=

==≤=.

当且仅当x=，即x=（x＞0）时等号成立.因此当x=时，tanα取得最大值，∠ACB取得最大值.

练习册系列答案

自主假期作业本吉林大学出版社系列答案

高中新课程寒假作业系列答案

海淀黄冈寒假作业合肥工业大学出版社系列答案

寒假Happy假日系列答案

寒假成长乐园系列答案

寒假创新型自主学习第三学期寒假衔接系列答案

寒假创新性自主学习寒假突破系列答案

寒假高效作业系列答案

寒假假期集训系列答案

寒假接力棒系列答案

相关题目

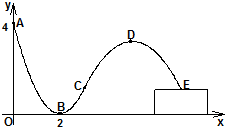轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动．如图，助跑道ABC是一段抛物线，某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处，飞行的轨迹是一段抛物线CDE（抛物线CDE与抛物线ABC在同一平面内），D为这段抛物线的最高点．现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系，x轴在地面上，助跑道一端点A（0，4），另一端点C（3，1），点B（2，0），单位：米．
（Ⅰ）求助跑道所在的抛物线方程；
（Ⅱ）若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线，为使运动员安全和空中姿态优美，要求运动员的飞行距离在4米到6米之间（包括4米和6米），试求运动员飞行过程中距离平台最大高度的取值范围？
（注：飞行距离指点C与点E的水平距离，即这两点横坐标差的绝对值．）

如右图所示，四边形ABCD是边长为6的正方形，SA⊥平面ABCD，SA=8，M是SA的中点，过M和BC的平面交SD于N．

　　(1)求二面角M－BC－D大小的正切值；

　　(2)求CN与平面ABCD所成角的正切值；

(3)求CN与BD所成角的余弦值；

(4)求平面SBC与SDC所成角大小的正弦值．

轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动．如图，助跑道ABC是一段抛物线，某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处，飞行的轨迹是一段抛物线CDE（抛物线CDE与抛物线ABC在同一平面内），D为这段抛物线的最高点．现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系，x轴在地面上，助跑道一端点A（0，4），另一端点C（3，1），点B（2，0），单位：米．
（Ⅰ）求助跑道所在的抛物线方程；
（Ⅱ）若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线，为使运动员安全和空中姿态优美，要求运动员的飞行距离在4米到6米之间（包括4米和6米），试求运动员飞行过程中距离平台最大高度的取值范围？
（注：飞行距离指点C与点E的水平距离，即这两点横坐标差的绝对值．）

（1）过一点向平面引垂线，________叫做这个点在这个平面内的射影；当这一点在平面内时，该点在平面上的射影就是它______；这一点与_______的线段叫做这点到这个平面的_______.如图所示，直线PQ⊥α,Q∈α,则点Q是______在平面α内的_____，线段_______是点_______到平面α的______.?

（2）一条直线和一个平面相交，但不______时，这条直线就叫做这个平面的_______，斜线与平面的交点叫做_____.从平面外一点向平面引斜线，这点与________间的线段叫做这点到这个平面的_______.如图所示，直线PR∩α=R,PR不______于α,直线PR是α的一条_____，点R为_______，线段_____是点P到α的______.?

（3）平面外一点到这个平面的垂线段______条，而这点到这个平面的______有无数条.?

（4）从斜线上斜足以外的一点向平面引垂线，过垂足的直线叫做斜线在这个平面内的_______，________与________间的线段叫做这点到平面的斜线段在这个平面内的________.如图所示，直线_____是直线PR在平面α上的______，线段______是点P到平面α的斜线段PR在平面α上的射影.?

（5）斜线上任意一点在平面上的射影一定在斜线的_____上.事实上，设a是平面α的斜线，B为斜足，在a上任取一点A，作AA₁⊥α,A₁是垂足，则A₁、B确定的直线a′是a在平面α内的______，如图所示，设P是a上任意一点，在a和AA₁确定的平面内，作PP₁∥AA₁,PP₁必与a′相交于一点P₁.∵AA₁α__________ ,PP_{1______________}AA₁，∴PP_{1__________}α.P₁为P在平面α上的射影，所以点P在平面α上的射影一定在直线a在平面α上的射影a′上.

如图所示，是圆的直径，是异于，

两点的圆周上的任意一点，垂直于圆所在的平

面，则，，，中，直角

三角形的个数是（　　）

A．1 B．2 C．3 D．4