题目内容
设z的共轭复数是 ,若Z+
,若Z+ =4,Z•
=4,Z• =8,则
=8,则 = .
= .
【答案】分析:设z=a+bi(a,b∈R),则 =a-bi.由于Z+
=a-bi.由于Z+ =4,Z•
=4,Z• =8,可得
=8,可得 ,解得a,b即可.
,解得a,b即可.
解答:解:设z=a+bi(a,b∈R),则 =a-bi.∵Z+
=a-bi.∵Z+ =4,Z•
=4,Z• =8,∴
=8,∴ ,解得
,解得 .
.
∴z=2±2i.
当z=2+2i时,则 =
= =
= =
= =
= =-i;
=-i;
同理,当z=2-i时, =i.
=i.
综上可知: =±i.
=±i.
故答案为±i.
点评:熟练掌握复数与共轭复数的定义、运算法则是解题的关键.
 =a-bi.由于Z+
=a-bi.由于Z+ =4,Z•
=4,Z• =8,可得
=8,可得 ,解得a,b即可.
,解得a,b即可.解答:解:设z=a+bi(a,b∈R),则
 =a-bi.∵Z+
=a-bi.∵Z+ =4,Z•
=4,Z• =8,∴
=8,∴ ,解得
,解得 .
.∴z=2±2i.
当z=2+2i时,则
 =
= =
= =
= =
= =-i;
=-i;同理,当z=2-i时,
 =i.
=i.综上可知:
 =±i.
=±i.故答案为±i.
点评:熟练掌握复数与共轭复数的定义、运算法则是解题的关键.

练习册系列答案
相关题目
 ,若
,若 ,
, ,则
,则 等于( )
等于( )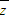 ,若
,若 ,
, ,则
,则 等于( )
等于( )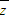 ,若
,若 ,
,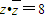 ,则
,则 等于( )
等于( )