题目内容
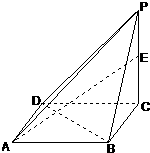已知四棱锥P-ABCD，底面是边长为1的正方形，侧棱PC长为2，且PC⊥底面ABCD，E是侧棱PC上的动点．
（Ⅰ） 求点C到平面PDB的距离；
（Ⅱ） 若点E为PC的中点，求平面ADE与平面ABE所成的锐二面角的大小．
分析：（I）点到平面的距离可以根据等体积法交线计算，即VP-BCD=VC-BPD，在换顶点求体积时应当换一个高与底面积都易求的顶点．
（II）建立空间直角坐标系，分别求出两个平面的法向量再结合向量的有关运算计算出二面角的平面角的余弦值，进而求出角度．
（II）建立空间直角坐标系，分别求出两个平面的法向量再结合向量的有关运算计算出二面角的平面角的余弦值，进而求出角度．
解答：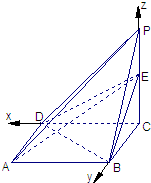
解：（I）四棱锥P-ABCD的底面是边长为1的正方形，
侧棱PC⊥底面ABCD，且PC=2．
设点C到平面PDB的距离为d，
∵VP-BCD=VC-BPD，
∴
S△BCD•PC=
S△BPD•dPD=PB=
，BD=
，
∴S△BPD=
，S△BCD=
∴d=
．
（II）以点C为坐标原点，CD所在的直线为x轴建立空间直角坐标系如图示：
则D（1，0，0），A（1，1，0），B（0，1，0），E（0，0，1），
从而
=(-1，0，1)，
=(0，1，0)，
=(1，0，0)，
=(0，-1，1)
设平面ADE和平面ABE的法向量分别为
=(a，b，c)，
=(a′，b′，c′)
由法向量的性质可得：-a+c=0，b=0，a'=0，-b'+c'=0
令c=1，c'=-1，则a=1，b'=-1，
∴
=(1，0，1)，
=(0，-1，-1)
设二面角D-AE-B的平面角为θ，则cosθ=
=-
∴θ=
．
解：（I）四棱锥P-ABCD的底面是边长为1的正方形，侧棱PC⊥底面ABCD，且PC=2．
设点C到平面PDB的距离为d，
∵VP-BCD=VC-BPD，
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 2 |
∴S△BPD=
| 3 |
| 2 |
| 1 |
| 2 |
∴d=
| 2 |
| 3 |
（II）以点C为坐标原点，CD所在的直线为x轴建立空间直角坐标系如图示：
则D（1，0，0），A（1，1，0），B（0，1，0），E（0，0，1），
从而
| DE |
| DA |
| BA |
| BE |
设平面ADE和平面ABE的法向量分别为
| m |
| n |
由法向量的性质可得：-a+c=0，b=0，a'=0，-b'+c'=0
令c=1，c'=-1，则a=1，b'=-1，
∴
| m |
| n |
设二面角D-AE-B的平面角为θ，则cosθ=
| ||||
|
| 1 |
| 2 |
∴θ=
| π |
| 3 |
点评：本题主要考查点到平面的距离与二面角的求法，解决此类问题的关键是熟悉几何体的结构特征，进而便于得到点、线、面的位置关系，也利用距离坐标系求解二面角．
练习册系列答案
快捷英语周周练系列答案
相关题目
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC，侧面PBC⊥底面ABCD，O是BC的中点．
已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，E为BC中点，AE与BD交于O点，AB=BC=2CD=2，BD⊥PE．
如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠DAB=∠ABC=90°，E是线段PC上一点，PC⊥平面BDE．