题目内容
 (理)如图,平面内有三个向量
(理)如图,平面内有三个向量| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OC |
| OA |
| OB |
| OC |
| 3 |
| OC |
| OA |
| OB |
分析:此题考查向量的加减法,数乘、数量积运算,关键是利用已知条件:
=λ
+μ
,将其平方.
| OC |
| OA |
| OB |
解答:解:∵
=λ
+μ
∴4λ2+4μ2-4λμ=48 ①
∵
与
的夹角为30度,
∴
*
=2√3*1*cos30°=3
即
*
=λ-
μ=3
∴λ2+
μ2-λμ=9
4λ2+μ2-4λμ=36 ②
由①②得,3μ2=12
∴μ=4或μ=-4
λ-
μ=6
∴μ=4,λ=8或者μ=-4,λ=4代入①式检验.符合
但是当λ=4,μ=-4是A、B、C三点共线,所以不符
故λ=8,μ=4
∴λ+μ=12
| OC |
| OA |
| OB |
∴4λ2+4μ2-4λμ=48 ①
∵
| OA |
| OC |
∴
| OC |
| OA |
即
| OC |
| OA |
| 1 |
| 2 |
∴λ2+
| 1 |
| 4 |
4λ2+μ2-4λμ=36 ②
由①②得,3μ2=12
∴μ=4或μ=-4
λ-
| 1 |
| 2 |
∴μ=4,λ=8或者μ=-4,λ=4代入①式检验.符合
但是当λ=4,μ=-4是A、B、C三点共线,所以不符
故λ=8,μ=4
∴λ+μ=12
点评:此题考查向量的基本运算,学生应熟练掌握向量的运算,是一道高考常见的题型

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目

 ,若OC=
,若OC= OA+
OA+ OB,
OB, 的值为 (
)
的值为 (
)
 D.4
D.4
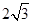 ,若OC=
,若OC= OA+
OA+ OB,
OB,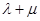 的值为 ( )
的值为 ( )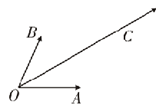
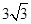 D.4
D.4