题目内容
已知双曲线
-
=1(b∈N*)的左、右两个焦点为F1、F2,P是双曲线上的一点,且满足|PF1||PF2|=|F1F2|2,|PF2|<4.
(1)求b的值;
(2)抛物线y2=2px(p>0)的焦点与该双曲线的右顶点重合,斜率为1的直线经过右顶点,与该抛物线交于A、B两点,求弦长|AB|.
【答案】
(1) b=1 (2)16
【解析】
解:(1)根据题意a2=4,a=2,又a2+b2=c2,
||PF1|-|PF2||=2a=4,
|PF1|·|PF2|=|F1F2|2=4c2,|PF2|<4,
得|PF2|2+4|PF2|-4c2=0在区间(0,4)上有解,
所以c2<8,因此b2<4,
又b∈N*,所以b=1.
(2)双曲线方程为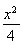
-y2=1,右顶点坐标为(2,0),
所以抛物线方程为y2=8x,①
直线方程为y=x-2,②
由①②两式联立,解得
和
所以弦长|AB|=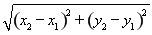
=16.
练习册系列答案
阅读快车系列答案
相关题目
=1(a＞0,b＞0)的动弦BC平行于虚轴，M、N是双曲线的左、右顶点,
=1(a＞b＞0)的左、右焦点分别为F1(-c,0)、F2(c,0)(c＞0),P是双曲线右支上的一点,
在
上的投影的绝对值恰好为|
|,且它们的夹角为
,则双曲线的离心率为
B.
+1 C.
D.2
=1（a＞0，b＞0）的离心率为
，右准线方程为
．
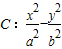=1（a＞0，b＞0）的离心率为
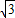，右准线方程为
．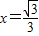