题目内容
设函数f(x)=ex,其中e为自然对数的底数.(Ⅰ)求函数g(x)=f(x)-ex的单调区间;
(Ⅱ)记曲线y=f(x)在点P(x,f(x))(其中x<0)处的切线为l,l与x轴、y轴所围成的三角形面积为S,求S的最大值.
【答案】分析:(Ⅰ)由函数的解析式,求出g'(x)=ex-e,利用导数求函数的单调区间,令导数大于0,解出增区间,令导数小于0,求出减区间.
(Ⅱ)由导数求出点P(x,f(x))(其中x<0)处的切线为l的方程,求出直线与x轴、y轴的交点坐标,将面积S表示出的函数,再利用导数研究它的最值
解答:解:(Ⅰ)由已知g(x)=ex-ex,
所以g'(x)=ex-e,…(1分)
由g'(x)=ex-e=0,得x=1,
所以,在区间(-∞,1)上,g'(x)<0,
函数g(x)在区间(-∞,1)上单调递减;
在区间(1,+∞)上,g'(x)>0,
函数g(x)在区间(1,+∞)上单调递增; …(4分)
即函数g(x)的单调递减区间为(-∞,1),单调递增区间为(1,+∞).
(Ⅱ)因为f'(x)=ex,
所以曲线y=f(x)在点P处切线为l: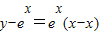 .…(6分)
.…(6分)
切线l与x轴的交点为(x-1,0),与y轴的交点为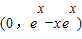 ,…(8分)
,…(8分)
因为x<0,所以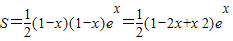 ,
,
∵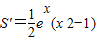 ,
,
∴在区间(-∞,-1)上,函数S(x)单调递增,在区间(-1,0)上,函数S(x)单调递减.…(10分)
所以,当x=-1时,S有最大值,此时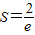 ,
,
所以,S的最大值为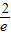 .…(12分)
.…(12分)
点评:本题考查利用导数研究函数的单调性,解答本题关键是理解导数与函数单调性的关系,此类题主要有两种类型,一是用导数研究单调性,一是由单调性得函数导数的符号,由此建立不等式求参数,本题的第一问属于此类,解答第二问时要注意数形结合
(Ⅱ)由导数求出点P(x,f(x))(其中x<0)处的切线为l的方程,求出直线与x轴、y轴的交点坐标,将面积S表示出的函数,再利用导数研究它的最值
解答:解:(Ⅰ)由已知g(x)=ex-ex,
所以g'(x)=ex-e,…(1分)
由g'(x)=ex-e=0,得x=1,
所以,在区间(-∞,1)上,g'(x)<0,
函数g(x)在区间(-∞,1)上单调递减;
在区间(1,+∞)上,g'(x)>0,
函数g(x)在区间(1,+∞)上单调递增; …(4分)
即函数g(x)的单调递减区间为(-∞,1),单调递增区间为(1,+∞).
(Ⅱ)因为f'(x)=ex,
所以曲线y=f(x)在点P处切线为l:
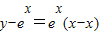 .…(6分)
.…(6分)切线l与x轴的交点为(x-1,0),与y轴的交点为
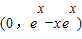 ,…(8分)
,…(8分)因为x<0,所以
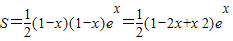 ,
,∵
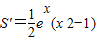 ,
,∴在区间(-∞,-1)上,函数S(x)单调递增,在区间(-1,0)上,函数S(x)单调递减.…(10分)
所以,当x=-1时,S有最大值,此时
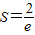 ,
,所以,S的最大值为
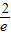 .…(12分)
.…(12分)点评:本题考查利用导数研究函数的单调性,解答本题关键是理解导数与函数单调性的关系,此类题主要有两种类型,一是用导数研究单调性,一是由单调性得函数导数的符号,由此建立不等式求参数,本题的第一问属于此类,解答第二问时要注意数形结合

练习册系列答案
相关题目