Question

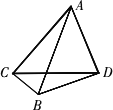
我国与某国联合举行反恐军事演习，演习内容是组织和实施在山地条件下对恐怖组织联合围歼作战行动．我军炮兵阵地位于地面A处，两观察所分别位于地面点C和点D处，已知CD＝6000米，∠ACD＝45°，∠ADC＝75°，目标出现在B处时，测得∠BCD＝30°，∠BDC＝15°，求炮兵阵地到目标的距离．

Answer 1

答案：
解析：

分析：如图，据题意知△ABD为直角三角形，要求AB，只需利用勾股定理求解即可，其中AD与BD可直接利用正弦定理分别在△ACD和△BCD中求出． 　　解：如图，在△ACD中，∠CAD＝180°－(45°＋75°)＝60°，CD＝6000，∠ACD＝45°． 　　根据正弦定理，得AD＝＝CD＝2000． 　　在△BCD中，∠CBD＝180°－(30°＋15°)＝135°，CD＝6000，∠BCD＝30°，根据正弦定理，得BD＝＝CD＝3000． 　　在△ABD中，∠ADB＝75°＋15°＝90°，所以△ABD为直角三角形． 　　根据勾股定理，可得AB＝＝1000(米)． 　　所以，炮兵阵地到目标的距离为1000米． 　　点评：利用正、余弦定理解决实际问题时，首先确定是在哪个三角形中(有时需对图形进行有效分割)，便于运用这两个定理；其次，观察用已知的角是否可以产生特殊三角形．