题目内容
设数列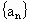 的首项
的首项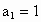 ,前n项和
,前n项和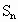 满足关系式
满足关系式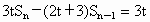 (t>0,n=2,3,4,…).
(t>0,n=2,3,4,…).
(1)求证:数列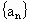 是等比数列;
是等比数列;
(2)设数列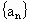 的公比为f(t),作数列
的公比为f(t),作数列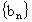 ,使
,使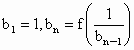 (n=2,3,4,…),求
(n=2,3,4,…),求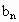 ;
;
(3)求和: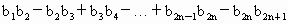 .
.
答案:略
解析:
提示:
解析:
|
解: (1)由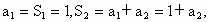 得 得
∴ 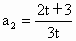 .于是 .于是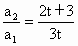 . ① . ①
由 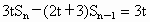 ,可知 ,可知
两式相减,得
∴ 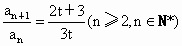 . ② . ②
由①②可知,对 nÎ N*,有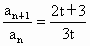 , ,
∴ 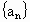 是一个首项为1,公比为 是一个首项为1,公比为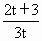 的等比数列. 的等比数列.
(2) 依题意,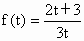 ,则 ,则
∴ 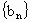 是首项为 是首项为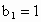 ,公差为 ,公差为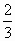 的等差数列. 的等差数列.
∴ 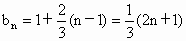 . .
(3) ∵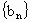 为等差数列, 为等差数列,
∴ 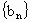 , ,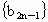 也等差数列,且公差均为 也等差数列,且公差均为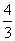 . .
而 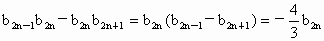 , ,
∴ 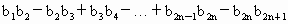
|
提示:
|
围绕 |

练习册系列答案
相关题目
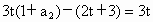
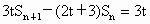
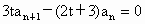

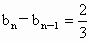
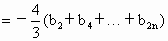
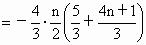
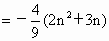
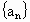 的首项
的首项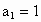 ,前n项和
,前n项和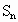 满足关系式
满足关系式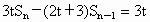 (t>0,n=2,3,4,…).
(t>0,n=2,3,4,…).
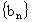 ,使
,使 (n=2,3,4,…),求
(n=2,3,4,…),求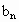 ;
;
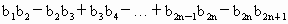 .
.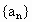 的首项
的首项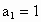 ,前n项的和
,前n项的和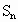 满足
满足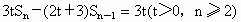
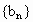 ,使
,使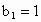 ,
,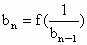 (n
(n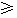 2),求:
2),求:
 的首项
的首项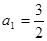 ,前n项和为Sn , 且满足
,前n项和为Sn , 且满足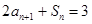 ( n∈N*) .则满足
( n∈N*) .则满足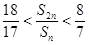 的所有n的和为
.
的所有n的和为
.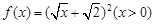 ,设正项数列
,设正项数列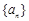 的首项
的首项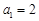 ,前n 项和
,前n 项和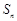 满足
满足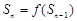 (
(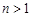 ,且
,且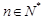 )。
)。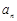 的表达式;
的表达式;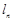 的斜率为
的斜率为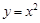 相切,
相切,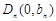 ,当
,当 ,若
,若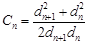 ,求数列
,求数列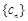 的前n 项和
的前n 项和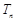 。
。