题目内容
已知点的序列An(xn,0),n∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(I)写出xn与xn-1、xx-2之间的关系式(n≥3);
(II)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
(III)求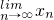 .
.
解:(I)当n≥3时,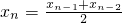
(II)a1=x2-x1=a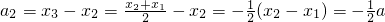
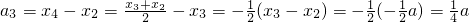 .
.
由此推测.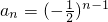 a(n∈N)
a(n∈N)
因为a1=a>0,且
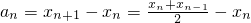 =
= (n≥2)
(n≥2)
所以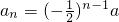 .
.
(III)解:当n≥3时,有xn=(xn-xn-1)+(xn-1-xn-2)+…+(x2-x1)+x1=an-1+an-2+…+a1,
由(II)知{an}是公比为 的等比数列,所以
的等比数列,所以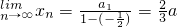 .
.
分析:(I)根据题意,An是线段An-2An-1的中点,可得xn与xn-1、xn-2之间的关系式,
(II)由题意知a1=a,a2=- a,a3=
a,a3= a,由此推测:an=(-
a,由此推测:an=(- )n-1a(n∈N*)再进行证明.
)n-1a(n∈N*)再进行证明.
(III)首先求出xn,然后根据(II)知{an}是公比为 的等比数列,求出结果.
的等比数列,求出结果.
点评:本题考查数列的性质和应用以及数列的极限,解题时要注意公式的灵活运用.属于中档题.
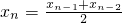
(II)a1=x2-x1=a
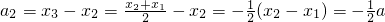
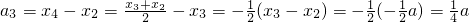 .
.由此推测.
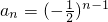 a(n∈N)
a(n∈N)因为a1=a>0,且
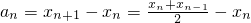 =
= (n≥2)
(n≥2)所以
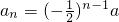 .
.(III)解:当n≥3时,有xn=(xn-xn-1)+(xn-1-xn-2)+…+(x2-x1)+x1=an-1+an-2+…+a1,
由(II)知{an}是公比为
 的等比数列,所以
的等比数列,所以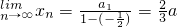 .
.分析:(I)根据题意,An是线段An-2An-1的中点,可得xn与xn-1、xn-2之间的关系式,
(II)由题意知a1=a,a2=-
 a,a3=
a,a3= a,由此推测:an=(-
a,由此推测:an=(- )n-1a(n∈N*)再进行证明.
)n-1a(n∈N*)再进行证明.(III)首先求出xn,然后根据(II)知{an}是公比为
 的等比数列,求出结果.
的等比数列,求出结果.点评:本题考查数列的性质和应用以及数列的极限,解题时要注意公式的灵活运用.属于中档题.

练习册系列答案
相关题目