题目内容
已知△BCD中,∠BCD=90°,AB⊥平面BCD,E、F分别是AC、AD上的动点,且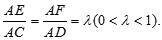
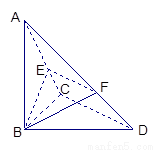
求证:不论λ为何值,总有平面BEF⊥平面ABC
【答案】
证明:∵AB⊥平面BCD, ∴AB⊥CD,∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC.
又
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF 平面BEF,
平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC.
【解析】本试题主要是考查了面面垂直运用,根据平行线分线段成比例定理,转化为EF∥CD是解决试题的关键。
由已知中AB⊥平面BCD,∠BCD=90°,由线面垂直的判定定理可得CD⊥平面ABC,由 AE:BC=AE:FD,根据平行线分线段成比例定理,可得EF∥CD,由线面垂直的第二判定定理可得EF⊥平面ABC,再由面面垂直的判定定理,可得平面BEF⊥平面ABC;

练习册系列答案
相关题目

 (2010•武昌区模拟)已知矩形ABCD中,AB=
(2010•武昌区模拟)已知矩形ABCD中,AB=
