题目内容
已知椭圆 上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线.
上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线.
(I)求椭圆C的方程;
(II)设直线l:y=kx+2与椭圆C交于不同的两点A、B,且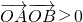 (其中O为坐标原点),求直线l的斜率k的取值范围.
(其中O为坐标原点),求直线l的斜率k的取值范围.
解:(I)设椭圆C的半焦距为c,
由题意得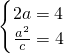 ,解得a=2,b=
,解得a=2,b= ,
,
∴椭圆C的方程为 ;
;
(II)设A(x1,y1),B(x2,y2),
联立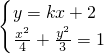 ,得(4k2+3)x2+16kx+4=0,
,得(4k2+3)x2+16kx+4=0,
∵直线l:y=kx+2与椭圆C交于不同的两点A、B,
∴△=(16k)2-16(4k2+3)>0,解得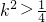 ,①
,①
且有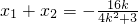 ,
,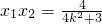 ,
,
∴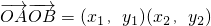 =x1x2+y1y2
=x1x2+y1y2
=x1x2+(kx1+2)(kx2+2)
=(1+k2)x1x2+2k(x1+x2)+4
=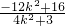 >0,
>0,
解得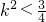 ,②
,②
由①②得,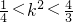 ,
,
解得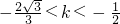 ,或
,或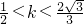 ,
,
∴斜率k的取值范围是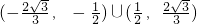 .
.
分析:(I)设椭圆C的半焦距为c,由题意得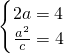 ,由此能够求出椭圆C的方程.
,由此能够求出椭圆C的方程.
(II)设A(x1,y1),B(x2,y2),由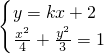 ,得(4k2+3)x2+16kx+4=0,由直线l:y=kx+2与椭圆C交于不同的两点A、B,解得
,得(4k2+3)x2+16kx+4=0,由直线l:y=kx+2与椭圆C交于不同的两点A、B,解得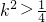 ,且有
,且有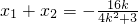 ,
,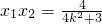 ,
,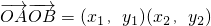 =
=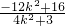 >0,解得
>0,解得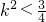 ,由此能够求出斜率k的取值范围.
,由此能够求出斜率k的取值范围.
点评:本题考查椭圆方程的求法,求直线斜率k的取值范围.解题时要认真审题,注意椭圆性质、韦达定理、不等式性质等知识点的灵活运用.
由题意得
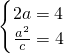 ,解得a=2,b=
,解得a=2,b= ,
,∴椭圆C的方程为
 ;
;(II)设A(x1,y1),B(x2,y2),
联立
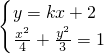 ,得(4k2+3)x2+16kx+4=0,
,得(4k2+3)x2+16kx+4=0,∵直线l:y=kx+2与椭圆C交于不同的两点A、B,
∴△=(16k)2-16(4k2+3)>0,解得
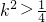 ,①
,①且有
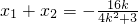 ,
,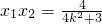 ,
,∴
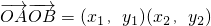 =x1x2+y1y2
=x1x2+y1y2=x1x2+(kx1+2)(kx2+2)
=(1+k2)x1x2+2k(x1+x2)+4
=
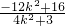 >0,
>0,解得
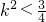 ,②
,②由①②得,
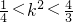 ,
,解得
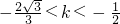 ,或
,或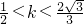 ,
,∴斜率k的取值范围是
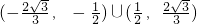 .
.分析:(I)设椭圆C的半焦距为c,由题意得
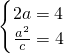 ,由此能够求出椭圆C的方程.
,由此能够求出椭圆C的方程.(II)设A(x1,y1),B(x2,y2),由
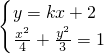 ,得(4k2+3)x2+16kx+4=0,由直线l:y=kx+2与椭圆C交于不同的两点A、B,解得
,得(4k2+3)x2+16kx+4=0,由直线l:y=kx+2与椭圆C交于不同的两点A、B,解得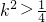 ,且有
,且有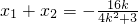 ,
,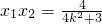 ,
,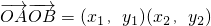 =
=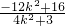 >0,解得
>0,解得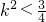 ,由此能够求出斜率k的取值范围.
,由此能够求出斜率k的取值范围.点评:本题考查椭圆方程的求法,求直线斜率k的取值范围.解题时要认真审题,注意椭圆性质、韦达定理、不等式性质等知识点的灵活运用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线.
上任意一点到两焦点距离之和为4,直线x+4=0为该椭圆的一条准线. (其中O为坐标原点),求直线l的斜率k的取值范围.
(其中O为坐标原点),求直线l的斜率k的取值范围.