Question

已知三棱锥S-ABC的各顶点都在一个半径为r的球面上，球心O在AB上，SO⊥底面ABC，AC=

2

r，则三棱锥的体积与球的体积之比是

1

4π

．

Answer 1

分析：由题意求出三棱锥底面ABC的面积，然后求出三棱锥的体积，再求出球的体积即可求出比值．

解答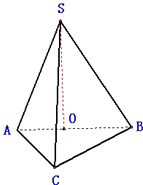：解：如图，已知三棱锥S-ABC的各顶点都在一个半径为r的球面上，球心O在AB上，
SO⊥底面ABC，AC=

2

r，⇒AB=2r，∠ACB=90°，BC=

2

r，
∴V_三棱锥=

1

3

×SO×S△ABC=

1

3

•r•

1

2

•

2

r•

2

r=

1

3

r3，V_球=

4

3

πr3，
∴V_三棱锥：V_球=

1

3

r3：

4

3

πr3=

1

4π

．
故答案为：

1

4π

．

点评：本题考查球的内接体的体积和球的体积的计算问题，注意转化思想的应用，是基础题．