题目内容

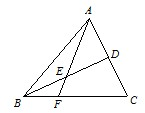精英家教网如图，在△ABC中，D是AC的中点，E是BD的中点，AE交BC于F，则
BF
FC
的值等于（　　）
A、
1
2
B、
1
3
C、
1
4
D、
2
5
分析：过D作DH∥AF交BC于H，根据已知中D是AC的中点，E是BD的中点，结合平行线分线段成比例定理可得，BF=FH=HC，进而得到
BF
FC
的值．
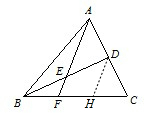解答：精英家教网解：过D作DH∥AF交BC于H
∵D是AC中点，
所以H是FC中点，FH=HC
E是BD中点，所以F是BH中点，
BF=FH
所以
BF
FC
=
1
2

故选A．
点评：本题考查的知识点是平行线等分线段定理，其中添加辅助线DH是解答本题的关键．
练习册系列答案
相关题目
精英家教网如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
AD=4cm．
（1）求：⊙O的直径BE的长；
（2）计算：△ABC的面积．
精英家教网如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=
3
BD，BC=2BD，则sinC的值为（　　）
A、
3
3
B、
3
6
C、
6
3
D、
6
6
如图，在△ABC中，设
AB
=a，
AC
=b，AP的中点为Q，BQ的中点为R，CR的中点恰为P．
（Ⅰ）若
AP
=λa+μb，求λ和μ的值；
（Ⅱ）以AB，AC为邻边，AP为对角线，作平行四边形ANPM，求平行四边形ANPM和三角形ABC的面积之比
S平行四边形ANPM
S△ABC
．
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
（1）求∠ADC的大小；
（2）求AB的长．
如图，在△ABC中，已知
BD
=2
DC
，则
AD
=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网