题目内容
已知椭圆的焦点在x轴上,短轴长为4,离心率为 .
.
(1)求椭圆的标准方程;
(2)若直线L方程为y=x+1,L交椭圆于M、N两点,求|MN|的长.
解:(1)设椭圆方程为 (a>b>0),
(a>b>0),
由椭圆短轴长为4得2b=4,解得b=2,
由离心率为 ,得
,得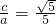 ,即a2=5c2=5(a2-4),解得a2=5,
,即a2=5c2=5(a2-4),解得a2=5,
所以椭圆的标准方程为 ;
;
(2)由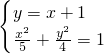 得9x2+10x-15=0,
得9x2+10x-15=0,
设M(x1,y1),N(x2,y2),则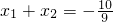 ,
,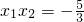 ,
,
所以|MN|=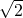 |x1-x2|=
|x1-x2|=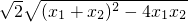 =
=
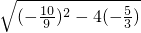 =
=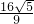 ;
;
分析:(1)设椭圆方程为 (a>b>0),由短轴长可得b值,由离心率为
(a>b>0),由短轴长可得b值,由离心率为 ,可得
,可得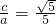 ,结合a2=b2+c2即可求得a值;
,结合a2=b2+c2即可求得a值;
(2)联立方程组消掉y得到x的二次方程,设M(x1,y1),N(x2,y2),由韦达定理及弦长公式即可求得弦长|MN|.
点评:本题考查直线与圆锥曲线的位置关系及椭圆方程的求解,弦长公式及韦达定理是解决该类题目的基础知识,要熟练掌握.
 (a>b>0),
(a>b>0),由椭圆短轴长为4得2b=4,解得b=2,
由离心率为
 ,得
,得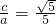 ,即a2=5c2=5(a2-4),解得a2=5,
,即a2=5c2=5(a2-4),解得a2=5,所以椭圆的标准方程为
 ;
;(2)由
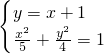 得9x2+10x-15=0,
得9x2+10x-15=0,设M(x1,y1),N(x2,y2),则
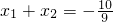 ,
,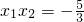 ,
,所以|MN|=
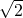 |x1-x2|=
|x1-x2|=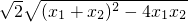 =
=
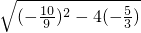 =
=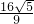 ;
;分析:(1)设椭圆方程为
 (a>b>0),由短轴长可得b值,由离心率为
(a>b>0),由短轴长可得b值,由离心率为 ,可得
,可得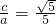 ,结合a2=b2+c2即可求得a值;
,结合a2=b2+c2即可求得a值;(2)联立方程组消掉y得到x的二次方程,设M(x1,y1),N(x2,y2),由韦达定理及弦长公式即可求得弦长|MN|.
点评:本题考查直线与圆锥曲线的位置关系及椭圆方程的求解,弦长公式及韦达定理是解决该类题目的基础知识,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目