题目内容
若函数 的最小值是-2,求实数a的值,并求出此时f(x)的最大值.
的最小值是-2,求实数a的值,并求出此时f(x)的最大值.
【答案】分析:利用同角三角函数的平方关系式,化简函数的表达式,即可用cosx表示f(x);换元t=cosx,0 则t∈[0,1],问题转化为二次函数闭区间上的最小值问题,通过分类
则t∈[0,1],问题转化为二次函数闭区间上的最小值问题,通过分类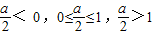 ,分别利用f(x)的最小值是-2,求实数a的值.
,分别利用f(x)的最小值是-2,求实数a的值.
解答:解:函数f(x)=(a-1)2-2sin2x-2acosx
=(a-1)2-2+cos2x-2acosx
=2cos2x-2acosx+a2-2a-1.令t=cosx,则t∈[0,1],
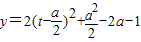 ,t∈[0,1]
,t∈[0,1]
①当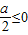 ,即a≤0时,
,即a≤0时,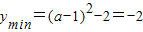 ,故a=1(舍)
,故a=1(舍)
②当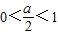 ,即0<a<2时,
,即0<a<2时,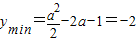
解得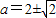 ,取
,取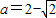 ,此时ymax=-1
,此时ymax=-1
③当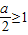 ,即a≥2时,
,即a≥2时,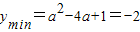
解得a=1(舍)或a=3,,此时ymax=2
综上,当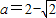 时ymax=-1;当a=3时ymax=2
时ymax=-1;当a=3时ymax=2
点评:本题考查换元法,分类讨论的数学思想,二次函数闭区间上的最值的应用,考查转化思想,计算能力.
 则t∈[0,1],问题转化为二次函数闭区间上的最小值问题,通过分类
则t∈[0,1],问题转化为二次函数闭区间上的最小值问题,通过分类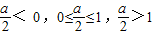 ,分别利用f(x)的最小值是-2,求实数a的值.
,分别利用f(x)的最小值是-2,求实数a的值.解答:解:函数f(x)=(a-1)2-2sin2x-2acosx
=(a-1)2-2+cos2x-2acosx
=2cos2x-2acosx+a2-2a-1.令t=cosx,则t∈[0,1],
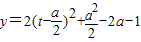 ,t∈[0,1]
,t∈[0,1]①当
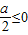 ,即a≤0时,
,即a≤0时,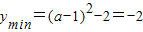 ,故a=1(舍)
,故a=1(舍)②当
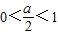 ,即0<a<2时,
,即0<a<2时,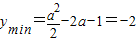
解得
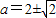 ,取
,取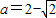 ,此时ymax=-1
,此时ymax=-1③当
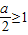 ,即a≥2时,
,即a≥2时,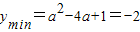
解得a=1(舍)或a=3,,此时ymax=2
综上,当
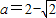 时ymax=-1;当a=3时ymax=2
时ymax=-1;当a=3时ymax=2点评:本题考查换元法,分类讨论的数学思想,二次函数闭区间上的最值的应用,考查转化思想,计算能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
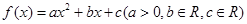 ,若函数
,若函数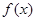 的最小值是
的最小值是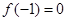 ,且
,且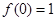 ,对称轴是
,对称轴是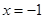 ,
,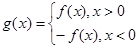 .
.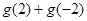 的值;
的值;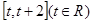 上的最小值.
上的最小值.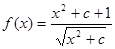 的最小值是2,则实数
的最小值是2,则实数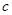 的取值范围是
的取值范围是