题目内容
已知直线l的方向向量为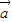
=（1，1），且过直线l1：2x+y+1=0和直线l2：x-2y+3=0的交点．（1）求直线l的方程；
（2）若点P（x，y）是曲线y=x2-lnx上任意一点，求点P到直线l的距离的最小值．
【答案】分析：（1）先求出两直线的交点，然后根据 直线的方向向量可求直线的斜率，即可求解直线方程
（2）当曲线上过点P的切线和直线y=x+2平行时，点P到直线y=x-2的距离最小．求出曲线对应的函数的导数，令导数值等于1，可得且点的坐标，此切点到直线y=x-2的距离即为所求．
解答：解：（1）由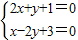
可得
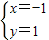
由题意可得，直线l的斜率k=1，且过（-1，1）
∴直线l的方程为y-1=x+1即x-y+2=0
（2）当过点P的切线和直线y=x+2平行时，点P到直线y=x+2的距离最小．
由题意可得，y′=2x-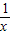
=1，
∴x=1，或 x=-
（舍去）
故曲线y=x2-lnx上和直线y=x+2平行的切线经过的切点坐标（1，1），
点（1，1）到直线y=x+2的距离d=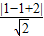
=
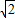
故点P到直线y=x-2的最小距离为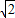
点评：本题考查点到直线的距离公式的应用，函数的导数的求法及导数的意义，体现了转化的数学思想．
（2）当曲线上过点P的切线和直线y=x+2平行时，点P到直线y=x-2的距离最小．求出曲线对应的函数的导数，令导数值等于1，可得且点的坐标，此切点到直线y=x-2的距离即为所求．
解答：解：（1）由
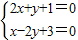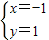
可得由题意可得，直线l的斜率k=1，且过（-1，1）
∴直线l的方程为y-1=x+1即x-y+2=0
（2）当过点P的切线和直线y=x+2平行时，点P到直线y=x+2的距离最小．
由题意可得，y′=2x-
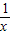=1，∴x=1，或 x=-
（舍去）故曲线y=x2-lnx上和直线y=x+2平行的切线经过的切点坐标（1，1），
点（1，1）到直线y=x+2的距离d=
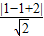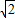
=故点P到直线y=x-2的最小距离为
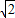
点评：本题考查点到直线的距离公式的应用，函数的导数的求法及导数的意义，体现了转化的数学思想．
练习册系列答案
相关题目
已知直线l的方向向量与向量
=（1，2）垂直，且直线l过点A（1，1），则直线l的方程为（ ）
| a |
| A、x-2y-1=0 |
| B、2x+y-3=0 |
| C、x+2y+1=0 |
| D、x+2y-3=0 |