题目内容
已知f(x)是偶函数,且在(-∞,0]上单调递减,对任意x∈R,x≠0,都有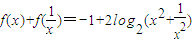 .
.(Ⅰ)指出f(x)在[0,+∞)上的单调性(不要求证明),并求f(1)的值;
(Ⅱ)k为常数,-1<k<1,解关于x的不等式
 .
.
【答案】分析:(Ⅰ)先利用偶函数的图象特点判断出f(x)在[0,+∞)上的单调性;再利用赋值法把1代入即可求出f(1)的值;
(Ⅱ)利用偶函数的性质以及f(1)的值,可以先把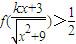 转化为
转化为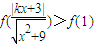 ,进而得到,
,进而得到,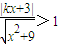 ⇒(1-k2)x2-6kx<0;再对二此项系数进行讨论即可解不等式.
⇒(1-k2)x2-6kx<0;再对二此项系数进行讨论即可解不等式.
解答:解:(Ⅰ)f(x)在[0,+∞)上是增函数,
∵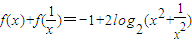 ,
,
∴f(1)+f(1)=-1+2log2(1+1)=1,
∴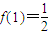 .
.
(Ⅱ)因为f(x)是偶函数,所以 ,
,
不等式就是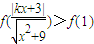 ,∵f(x)在[0,+∞)上递增,∴
,∵f(x)在[0,+∞)上递增,∴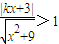 ∴
∴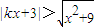 ,
,
k2x2+6kx+9>x2+9.∴(1-k2)x2-6kx<0,
①若k=0,则x2<0,∴不等式解集为ϕ;
②若-1<k<0,则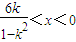 ,∴不等式解集为
,∴不等式解集为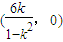 ;
;
③若0<k<1,则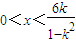 ,∴不等式解集为
,∴不等式解集为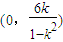 .
.
点评:本题主要考查函数单调性和奇偶性的综合应用问题.偶函数的图象特点是在关于原点对称的区间上单调性相反;而奇函数的图象特点是在关于原点对称的区间上单调性相同.
(Ⅱ)利用偶函数的性质以及f(1)的值,可以先把
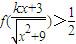 转化为
转化为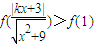 ,进而得到,
,进而得到,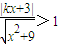 ⇒(1-k2)x2-6kx<0;再对二此项系数进行讨论即可解不等式.
⇒(1-k2)x2-6kx<0;再对二此项系数进行讨论即可解不等式.解答:解:(Ⅰ)f(x)在[0,+∞)上是增函数,
∵
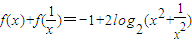 ,
,∴f(1)+f(1)=-1+2log2(1+1)=1,
∴
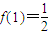 .
.(Ⅱ)因为f(x)是偶函数,所以
 ,
,不等式就是
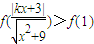 ,∵f(x)在[0,+∞)上递增,∴
,∵f(x)在[0,+∞)上递增,∴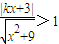 ∴
∴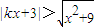 ,
,k2x2+6kx+9>x2+9.∴(1-k2)x2-6kx<0,
①若k=0,则x2<0,∴不等式解集为ϕ;
②若-1<k<0,则
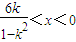 ,∴不等式解集为
,∴不等式解集为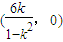 ;
;③若0<k<1,则
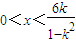 ,∴不等式解集为
,∴不等式解集为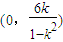 .
.点评:本题主要考查函数单调性和奇偶性的综合应用问题.偶函数的图象特点是在关于原点对称的区间上单调性相反;而奇函数的图象特点是在关于原点对称的区间上单调性相同.

练习册系列答案
相关题目
已知f(x)是偶函数,且f(x)在[0,+∞)上是增函数,如果f(ax+1)≤f(x-2)在x∈[
,1]上恒成立,则实数a的取值范围是( )
| 1 |
| 2 |
| A、[-2,1] |
| B、[-5,0] |
| C、[-5,1] |
| D、[-2,0] |