题目内容
已知α，β为锐角，且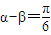
，那么sinαsinβ的取值范围是 ．
【答案】分析：先通过积化和差公式和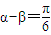
，，求得sinαsinβ=-
[cos（2β
）-
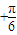]再根据β的范围求出cos（2β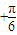
）的范围，进而求出sinαsinβ的取值范围．
解答：解：∵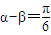
∴sinαsinβ=-
[cos（α+β）-cos（α-β）]=-
[cos（α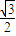+β）-
]=-
[cos（2β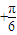
）-
]
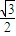∵β为锐角，即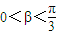
∴
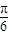＜2β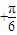
＜
，
∴-
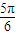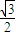≤cos（2β
）＜
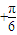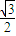
∴0＜-
[cos（2β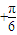
）-
]≤
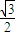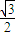
故答案为：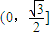
点评：本题主要考查三角函数中的积化和差公式的应用，属基础题．
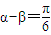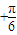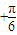，，求得sinαsinβ=-[cos（2β）-]再根据β的范围求出cos（2β）的范围，进而求出sinαsinβ的取值范围．解答：解：∵
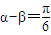
∴sinαsinβ=-
[cos（α+β）-cos（α-β）]=-[cos（α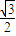+β）-]=-[cos（2β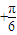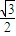）-]∵β为锐角，即
∴
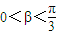
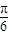＜2β＜，∴-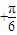
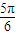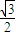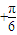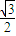
≤cos（2β）＜∴0＜-
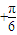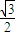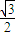
[cos（2β）-]≤故答案为：
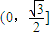
点评：本题主要考查三角函数中的积化和差公式的应用，属基础题．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
已知sinβ=
，β为锐角，且sin(α+β)=cosα，则tan(α+β)=（ ）
| 3 |
| 5 |
| A、1 | ||
B、
| ||
| C、-2 | ||
| D、2 |
已知α，β，γ均为锐角，且tanα=
，tanβ=
，tanγ=
，则α，β，γ的和为（ ）
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x，y为锐角，且满足cos x=
，cos（x+y）=
，则sin y的值是（ ）
| 4 |
| 5 |
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|