题目内容
已知线性方程组的增广矩阵为
|
分析:将原方程组写成矩阵形式为Ax=b,其中A为3×3方阵,x为3个变量构成列向量,b为3个常数项构成列向量. 而当它的系数矩阵D奇异时,或者说行列式D=0时,方程组有无数个解或无解.由此求得a值.
解答:解:系数矩阵D奇异时,或者说行列式D=0时,方程组有无数个解或无解.
∴系数行列式D=0,
即
=0.
解之得:a=2
故答案为:2.
∴系数行列式D=0,
即
|
解之得:a=2
故答案为:2.
点评:本题主要考查系数矩阵的逆矩阵解方程组及克莱姆法则,克莱姆法则不仅仅适用于实数域,它在任何域上面都可以成立.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
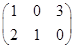 ,则其对应的方程组为_____________
,则其对应的方程组为_____________ ,则其对应的方程组为 .
,则其对应的方程组为 .