题目内容
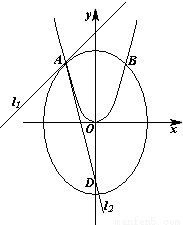
如图,已知曲线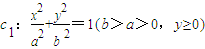 与抛物线c2:x2=2py(p>0)的交点分别为A、B,曲线c1和抛物线c2在点A处的切线分别为l1、l2,且l1、l2的斜率分别为k1、k2.
与抛物线c2:x2=2py(p>0)的交点分别为A、B,曲线c1和抛物线c2在点A处的切线分别为l1、l2,且l1、l2的斜率分别为k1、k2.(Ⅰ)当
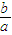 为定值时,求证k1•k2为定值(与p无关),并求出这个定值;
为定值时,求证k1•k2为定值(与p无关),并求出这个定值;(Ⅱ)若直线l2与y轴的交点为D(0,-2),当a2+b2取得最小值9时,求曲线c1和c2的方程.
【答案】分析:(Ⅰ)利用导数分别求l1、l2的斜率分别为k1、k2.进而可求k1•k2,利用点A在曲线c1和抛物线c2上,结合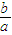 为定值时可得结论.
为定值时可得结论.
(Ⅱ)设A点的坐标为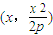 ,利用l2过点D(0,-2),则x2=4p,从而可求点
,利用l2过点D(0,-2),则x2=4p,从而可求点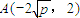 的坐标代入曲线c1的方程得
的坐标代入曲线c1的方程得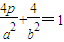 .从而利用基本不等式可求a2+b2最小值,注意等号成立的条件.
.从而利用基本不等式可求a2+b2最小值,注意等号成立的条件.
解答:解:(Ⅰ)设点A的坐标为(x,y),
由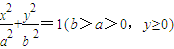 得:
得: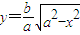
则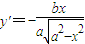 ,∴
,∴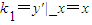 …2′
…2′
由x2=2py(p>0)得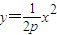 ,∴
,∴ …4′
…4′
∴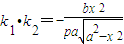
又∵x2=2py,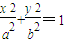 ,∴
,∴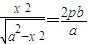 .
.
∴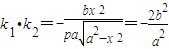 为定值.…6′
为定值.…6′
(Ⅱ)如图设A点的坐标为 ,则x∈(-a,0).
,则x∈(-a,0).
由(Ⅰ)知: ,则直线
,则直线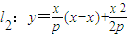 .
.
∵l2过点D(0,-2),则x2=4p,即 ,∴点
,∴点 .…8′
.…8′
将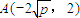 代入曲线c1的方程得
代入曲线c1的方程得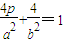 .
.
∴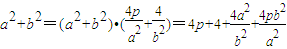 .
.
由重要不等式得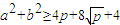 .…10′
.…10′
当且仅当“=”成立时,有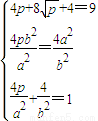 ,解得
,解得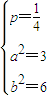
∴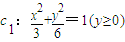 ,c2:y=2x2.…13′
,c2:y=2x2.…13′
点评:本题的考点是直线与圆锥曲线的综合问题,主要考查椭圆与抛物线的位置关系,考查利用基本不等式求最值.
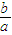 为定值时可得结论.
为定值时可得结论.(Ⅱ)设A点的坐标为
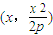 ,利用l2过点D(0,-2),则x2=4p,从而可求点
,利用l2过点D(0,-2),则x2=4p,从而可求点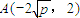 的坐标代入曲线c1的方程得
的坐标代入曲线c1的方程得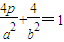 .从而利用基本不等式可求a2+b2最小值,注意等号成立的条件.
.从而利用基本不等式可求a2+b2最小值,注意等号成立的条件.解答:解:(Ⅰ)设点A的坐标为(x,y),
由
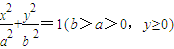 得:
得: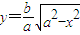
则
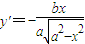 ,∴
,∴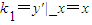 …2′
…2′由x2=2py(p>0)得
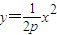 ,∴
,∴ …4′
…4′∴
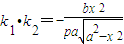
又∵x2=2py,
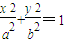 ,∴
,∴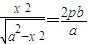 .
.∴
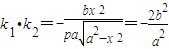 为定值.…6′
为定值.…6′(Ⅱ)如图设A点的坐标为
 ,则x∈(-a,0).
,则x∈(-a,0).由(Ⅰ)知:
 ,则直线
,则直线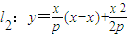 .
.∵l2过点D(0,-2),则x2=4p,即
 ,∴点
,∴点 .…8′
.…8′将
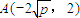 代入曲线c1的方程得
代入曲线c1的方程得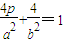 .
.∴
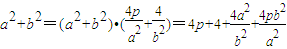 .
.由重要不等式得
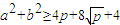 .…10′
.…10′当且仅当“=”成立时,有
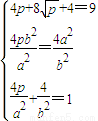 ,解得
,解得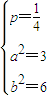
∴
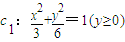 ,c2:y=2x2.…13′
,c2:y=2x2.…13′点评:本题的考点是直线与圆锥曲线的综合问题,主要考查椭圆与抛物线的位置关系,考查利用基本不等式求最值.

练习册系列答案
相关题目
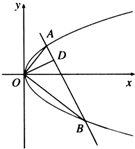 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1),求p的值.
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1),求p的值.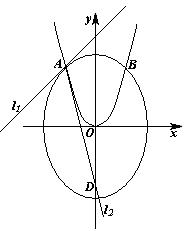
 与抛物线
与抛物线 相交于
相交于 两点,与
两点,与 轴相交于点
轴相交于点 ,若
,若 .(1)求证:
.(1)求证:
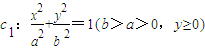 与抛物线c2:x2=2py(p>0)的交点分别为A、B,曲线c1和抛物线c2在点A处的切线分别为l1、l2,且l1、l2的斜率分别为k1、k2.
与抛物线c2:x2=2py(p>0)的交点分别为A、B,曲线c1和抛物线c2在点A处的切线分别为l1、l2,且l1、l2的斜率分别为k1、k2.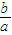 为定值时,求证k1•k2为定值(与p无关),并求出这个定值;
为定值时,求证k1•k2为定值(与p无关),并求出这个定值;