题目内容
{an}是等差数列,若a1,a3,a4是等比数列{bn}的连续三项,则{bn}的公比为 .
【答案】分析:{an}是等差数列,推出a3=a1+2d,a4=a1+3d,利用a1,a3,a4是等比数列{bn}的连续三项,得到(a1+2d)2=a1(a1+3d),求出d=-4a1或d=0.然后求出{bn}的公比q即可.
解答:解:∵{an}是等差数列,设公差为d,则a3=a1+2d,a4=a1+3d
∵a1,a3,a4是等比数列{bn}的连续三项,
∴a32=a1×a4,
即(a1+2d)2=a1(a1+3d),
解得a1=-4d,或d=0
当a1=-4d时,{bn}的公比q= =
=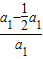 =
=
当d=0时,{bn}的公比q=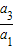 =1
=1
∴{bn}的公比为 或1
或1
故答案为: 或1
或1
点评:本题考查了等差数列的定义及其通项公式,等比数列的定义及其通项公式,公比的定义及其性质.
解答:解:∵{an}是等差数列,设公差为d,则a3=a1+2d,a4=a1+3d
∵a1,a3,a4是等比数列{bn}的连续三项,
∴a32=a1×a4,
即(a1+2d)2=a1(a1+3d),
解得a1=-4d,或d=0
当a1=-4d时,{bn}的公比q=
 =
=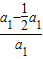 =
=
当d=0时,{bn}的公比q=
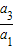 =1
=1∴{bn}的公比为
 或1
或1故答案为:
 或1
或1点评:本题考查了等差数列的定义及其通项公式,等比数列的定义及其通项公式,公比的定义及其性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目