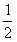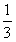题目内容
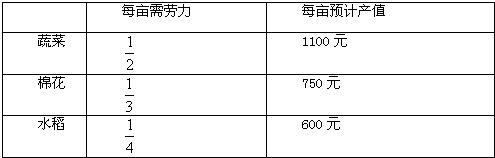
20个下岗职工开了50亩荒地，这些地可以种蔬菜、棉花、水稻，如果种这些农作物每亩地所需的劳动力和预计的产值如下：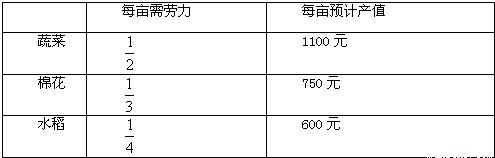
问怎样安排，才能使每亩地都种上作物，所有职工都有工作，而且农作物的预计总产值达到最高？
【答案】分析：先设种蔬菜、棉花，水稻分别为x亩，y亩，z亩，总产值为u，依题意得列出约束条件和目标函数，最后依据线性规则的方法求出目标函数的最大值即可．
解答：解：设种蔬菜、棉花，水稻分别为x亩，y亩，z亩，总产值为u，依题意得
约束条件是
，目标函数是u=1100x+750y+600z
①②联立解得y=90-3x，z=2x-40代入目标函数得u=43500+50x．
因为x，y，z≥0，
∴y=90-3x≥0，z=2x-40≥0，得20≤x≤30，
所以当x=30时，u取最大值45000，此时y=0，z=20
所以安排15个职工种30亩蔬菜，5个职工种20亩水稻，可使产值高达45000元．
点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想，属中档题．
解答：解：设种蔬菜、棉花，水稻分别为x亩，y亩，z亩，总产值为u，依题意得
约束条件是
，目标函数是u=1100x+750y+600z①②联立解得y=90-3x，z=2x-40代入目标函数得u=43500+50x．
因为x，y，z≥0，
∴y=90-3x≥0，z=2x-40≥0，得20≤x≤30，
所以当x=30时，u取最大值45000，此时y=0，z=20
所以安排15个职工种30亩蔬菜，5个职工种20亩水稻，可使产值高达45000元．
点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想，属中档题．
练习册系列答案
名校课堂系列答案
相关题目
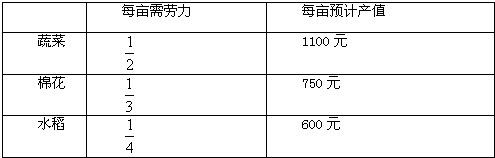
20个下岗职工开了50亩荒地，这些地可以种蔬菜、棉花、水稻，如果种这些农作物每亩地所需的劳力和预计的产值如下：
| 每亩需劳力 | 每亩预计产值 | |
| 蔬 菜 |
| 1100元 |
| 棉 花 |
| 750元 |
| 水 稻 |
| 600元 |
问怎样安排，才能使每亩地都种上作物，所有职工都有工作，而且农作物的预计总产值达到最高？
