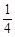Question

设a是从集合{1，2，3，4}中随机取出的一个数，b是从集合{1，2，3}中随机取出的一个数，构成一个基本事件（a，b）．记“在这些基本事件中，满足log_ba≥1为事件A，则A发生的概率是

5

12

．

Answer 1

分析：先求出基本事件的总数，然后例举出满足log_ba≥1的基本事件，最后根据古典概型的概率公式进行求解即可．

解答：解：由已知得基本事件（a，b）共有4×3=12（个）
满足log_ba≥1，即a≥b＞1的基本事件有（4，2），（4，3），（3，2），（3，3），（2，2）共5个，
故P=

5

12

．
故答案为：

5

12

点评：本题主要考查了等可能事件的概率，以及古典概型的概率公式，属于基础题．