题目内容
定义在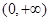 上的函数
上的函数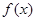 ,对于任意的m,n∈(0,+∞),都有
,对于任意的m,n∈(0,+∞),都有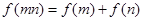 成立,当x>1时,
成立,当x>1时,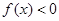 .
.
(1)求证:1是函数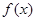 的零点;
的零点;
(2)求证: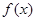 是(0,+∞)上的减函数;
是(0,+∞)上的减函数;
(3)当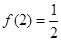 时,解不等式
时,解不等式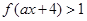 .
.
【答案】
(3)当a=0时,解集为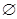 ;当a>0时,解集为
;当a>0时,解集为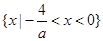 ;
;
当a<0时,解集为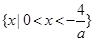 ..
..
【解析】(1)赋值法,求得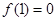 ;(2)注意构造
;(2)注意构造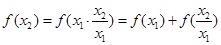 ;
;
(3)由 等价于
等价于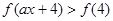 ,分类讨论.
,分类讨论.
解:(1)对于任意的正实数m,n都有 成立,
成立,
所以令m=n=1,则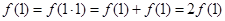 .
.
∴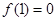 ,即1是函数f(x)的零点.
(3分)
,即1是函数f(x)的零点.
(3分)
(2)设0<x1<x2,则由于对任意正数 ,
,
所以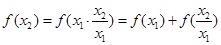 ,即
,即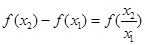
又当x>1时,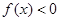 ,而
,而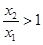 .所以
.所以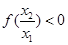 .
.
从而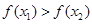 ,因此
,因此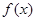 在(0,+∞)上是减函数.
(7分)
在(0,+∞)上是减函数.
(7分)
(3)根据条件有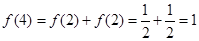 ,
,
所以 等价于
等价于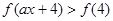 .
.
再由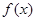 是定义在(0,+∞)上的减函数,所以0<ax+4<4.即
是定义在(0,+∞)上的减函数,所以0<ax+4<4.即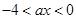 . (9分)
. (9分)
当a=0时,-4<0<0不成立,此时不等式的解集为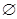 ; (10分)
; (10分)
当a>0时,-4<ax<0,即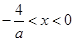 ,此时不等式的解集为
,此时不等式的解集为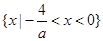 ;
;
当a<0时,-4<ax<0,即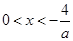 ,此时不等式的解集为
,此时不等式的解集为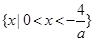 .(12分)
.(12分)

练习册系列答案
相关题目
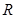 上的函数
上的函数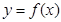 ,对于任意的实数
,对于任意的实数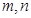 ,恒有
,恒有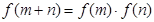 ,且当
,且当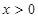 时,
时,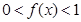 。
。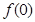 及
及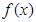 的值域。
的值域。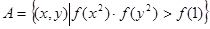 ,
,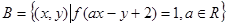 ,
,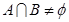 ,求
,求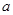 的范围。
的范围。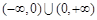 上的函数
上的函数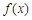 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列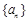 ,
,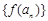 仍是等比数列,则称
仍是等比数列,则称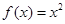 ; ②
; ②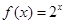 ; ③
; ③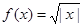 ; ④
; ④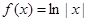 .
. 的序号为
的序号为