题目内容
下列有四个命题：正确为（ ）
①α，β表示两个不同平面，l表示直线，“若α⊥β，则l?α，l⊥β”的逆命题；
②“若a，b是偶数，则a+b是偶数”的否命题；
③“在△ABC中，若
B•
C＜0，则△ABC为钝角三角形”的逆否命题；
④“梯形的对角线是相等的”．
①α，β表示两个不同平面，l表示直线，“若α⊥β，则l?α，l⊥β”的逆命题；
②“若a，b是偶数，则a+b是偶数”的否命题；
③“在△ABC中，若
| A |
| A |
④“梯形的对角线是相等的”．
分析：①α，β表示两个不同平面，l表示直线，“若α⊥β，则l?α，l⊥β”的逆命题，先写出它的否命题，须同时对条件和结论同时进行否定，再判断它的正确性．②先写出“若a，b是偶数，则a+b是偶数”的否命题，再进行判断；对于③
•
＜0，则角A为钝角，可判定原命题的真假，从而对其逆否命题的真假．④“梯形的对角线是相等的”是错的．
| AB |
| AC |
解答：解：①“若α⊥β，则l?α，l⊥β”的逆命题是：“若l?α，l⊥β，则α⊥β”，根据面面垂直的判断定理得出其是正确的；
②条件和结论同时进行否定，则否命题为：若a，b不都是偶数，则a+b不是偶数，是错误的．
③若
•
＜0，则角A为钝角，从而△ABC为钝角三角形，故正确，从而其逆否命题正确．
④“梯形的对角线不一定是相等的”故错．
综上①③是正确命题
故选B．
②条件和结论同时进行否定，则否命题为：若a，b不都是偶数，则a+b不是偶数，是错误的．
③若
| AB |
| AC |
④“梯形的对角线不一定是相等的”故错．
综上①③是正确命题
故选B．
点评：本题考查了四种命题的真假关系．命题的否定就是对这个命题的结论进行否认（命题的否定与原命题真假性相反）；命题的否命题就是对这个命题的条件和结论进行否认（否命题与原命题的真假性没有必然联系）．
练习册系列答案
智慧小复习系列答案
相关题目
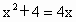的解集可表示为｛2，2｝．
的解集可表示为｛2，2｝．
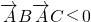，则△ABC为钝角三角形”的逆否命题；
，则△ABC为钝角三角形”的逆否命题；