题目内容
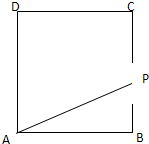 动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D再回到A,设x表示P点的行程,g(x)表示△ABP的面积,求g(x)并作出g(x)的简图.
动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D再回到A,设x表示P点的行程,g(x)表示△ABP的面积,求g(x)并作出g(x)的简图.分析:根据点P在AB、BC、CD、DA上运动时,求出S△ABP的表达式g(x),并画出g(x)的图象即可.
解答:解:当P在线段AB上时,即0≤x≤1时,△ABP的面积为0;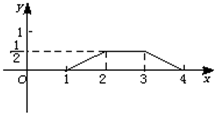
当P在BC上时,即1<x≤2时,S△ABP=
AB•BP=
(x-1);
当P在CD上时,即2<x≤3时,S△ABP=
;
当P在DA上时,即3<x≤4时,S△ABP=
(4-x);
∴g(x)=
;
画出g(x)的图象,如图.

当P在BC上时,即1<x≤2时,S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
当P在CD上时,即2<x≤3时,S△ABP=
| 1 |
| 2 |
当P在DA上时,即3<x≤4时,S△ABP=
| 1 |
| 2 |
∴g(x)=
|
画出g(x)的图象,如图.
点评:本题考查了求分段函数的解析式与画出函数的图象等问题,是基础题.

练习册系列答案
相关题目
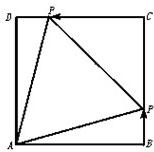 动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.
动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.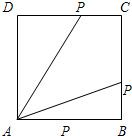 动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D再回到A,试写出线段AP的长度y与P点的行路程x之间的函数关系式.
动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D再回到A,试写出线段AP的长度y与P点的行路程x之间的函数关系式.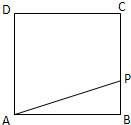 如图,动点P从边长为1的正方形ABCD的顶点A开始,顺次经B、C、D绕边界一周,当x表示点P的行程,y表示PA之长时,
如图,动点P从边长为1的正方形ABCD的顶点A开始,顺次经B、C、D绕边界一周,当x表示点P的行程,y表示PA之长时,