题目内容
在△ABC中,已知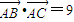 ,sinB=cosAsinC,又△ABC的面积等于6.
,sinB=cosAsinC,又△ABC的面积等于6.(1)求△ABC的三边之长;
(2)设P是△ABC(含边界)内一点,P到三边AB、BC、CA的距离分别为d1、d2、d3,求d1+d2+d3的取值范围.
【答案】分析:(1)设三边分别为a,b,c,利用正弦定理和余弦定理将题中条件角的关系转化成边的关系,得到直角三角形ABC,再结合向量条件利用三角形面积公式即可求出三边长.
(2)欲求d1+d2+d3的取值范围,利用坐标法,将三角形ABC放置在直角坐标系中,通过点到直线的距离将求d1+d2+d3的范围转化为故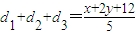 .最后结合线性规划的思想方法求出范围即可.
.最后结合线性规划的思想方法求出范围即可.
解答: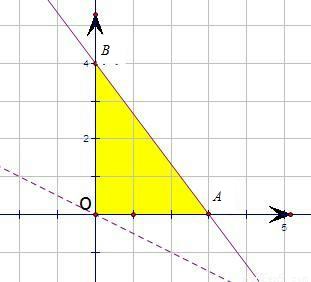 解:(1)设三角形三内角A、B、C对应的三边分别为a,b,c,
解:(1)设三角形三内角A、B、C对应的三边分别为a,b,c,
∵sinB=cosAsinC,∴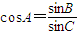 ,由正弦定理有
,由正弦定理有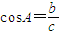 ,
,
又由余弦定理有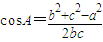 ,∴
,∴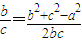 ,即a2+b2=c2,
,即a2+b2=c2,
所以△ABC为Rt△ABC,且∠C=90°(3分)
又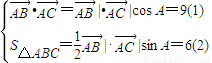
(1)÷(2),得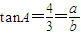 (4分)
(4分)
令a=4k,b=3k(k>0)
则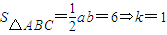 ∴三边长分别为3,4,5(6分)
∴三边长分别为3,4,5(6分)
(2)以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,
则A、B坐标为(3,0),(0,4),直线AB方程为4x+3y-12=0.
设P点坐标为(x,y),则由P到三边AB、BC、AB的距离为d1,d2和d3
可知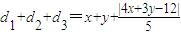 ,(8分)
,(8分)
且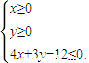 故
故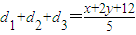 .(10分)
.(10分)
令m=x+2y,由线性规划知识可知,如图:
当直线分别经过点A、O时,z取得最大、最小值.
故0≤m≤8,故d1+d2+d3的取值范围是 (12分)
(12分)
点评:本题主要考查了解三角形中正弦定理、余弦定理、平面向量数量积的运算、简单线性规划思想方法的应用,属于中档题.
(2)欲求d1+d2+d3的取值范围,利用坐标法,将三角形ABC放置在直角坐标系中,通过点到直线的距离将求d1+d2+d3的范围转化为故
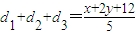 .最后结合线性规划的思想方法求出范围即可.
.最后结合线性规划的思想方法求出范围即可.解答:
 解:(1)设三角形三内角A、B、C对应的三边分别为a,b,c,
解:(1)设三角形三内角A、B、C对应的三边分别为a,b,c,∵sinB=cosAsinC,∴
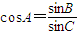 ,由正弦定理有
,由正弦定理有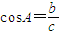 ,
,又由余弦定理有
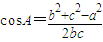 ,∴
,∴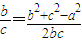 ,即a2+b2=c2,
,即a2+b2=c2,所以△ABC为Rt△ABC,且∠C=90°(3分)
又
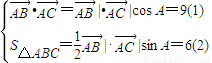
(1)÷(2),得
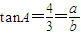 (4分)
(4分)令a=4k,b=3k(k>0)
则
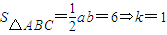 ∴三边长分别为3,4,5(6分)
∴三边长分别为3,4,5(6分)(2)以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,
则A、B坐标为(3,0),(0,4),直线AB方程为4x+3y-12=0.
设P点坐标为(x,y),则由P到三边AB、BC、AB的距离为d1,d2和d3
可知
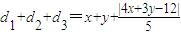 ,(8分)
,(8分)且
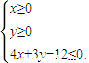 故
故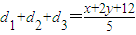 .(10分)
.(10分)令m=x+2y,由线性规划知识可知,如图:
当直线分别经过点A、O时,z取得最大、最小值.
故0≤m≤8,故d1+d2+d3的取值范围是
 (12分)
(12分)点评:本题主要考查了解三角形中正弦定理、余弦定理、平面向量数量积的运算、简单线性规划思想方法的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目