题目内容
已知向量a＝（cosx,sinx）,b＝(-cosx,cosx),c＝(-1,0).（1）若x=
，求向量a、c的夹角；
（2）当x∈［
,
］时，求函数f(x)=2a·b+1的最大值.
解:（1）当x=时，
cos〈a，c〉=
=.
∵0≤〈a,c〉≤π,∴〈a，c〉=
.
（2）f(x)=2a·b+1=2(-cos2x+sinxcosx)+1=2sinxcosx-(2cos2x-1)
=sin2x-cos2x=
sin(2x-
).
∵x∈［
,
］,2x-
∈［
,2π］,
∴sin(2x-
)∈［-1,
］.
∴当2x-
=
,
即x=
时，f(x)max=1.
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
），且a⊥b． 
)的值．
．
），且a⊥b． 
)的值．
已知向量a＝(cos
x，sin
，sin
，－1)，其中x∈R，
时，求x值的集合；
.
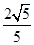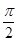<β<0<α<
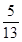，求sinα的值．